
【题目】解下列方程:
(1)4-![]() m=-m; (2)56-8x=11+x;
m=-m; (2)56-8x=11+x;
(3) ![]() x+1=5+
x+1=5+![]() x; (4)-5x+6+7x=1+2x-3+8x.
x; (4)-5x+6+7x=1+2x-3+8x.
【答案】(1) m=-10;(2)x=5;(3)x=4;(4)x=1.
【解析】试题分析:(1)移项、合并同类项后,系数化为1即可得方程的解;(2)移项、合并同类项后,系数化为1即可得方程的解;(3)移项、合并同类后项即可得方程的解;(4)移项、合并同类项后,系数化为1即可得方程的解.
试题解析:
(1) 移项,得-![]() m+m=-4.
m+m=-4.
合并同类项,得![]() m=-4.
m=-4.
系数化为1,得m=-10.
(2) 移项,得-8x-x=11-56.
合并同类项,得-9x=-45.
系数化为1,得x=5.
(3) 移项,得![]() x-
x-![]() x=5-1.
x=5-1.
合并同类项,得x=4.
(4) 移项,得-5x+7x-2x-8x=1-3-6.
合并同类项,得-8x=-8.
系数化为1,得x=1.


科目:初中数学 来源: 题型:
【题目】某一线城市对出租车营运价进行了调整,调价前后的收费标准对比如下:调整前,3公里及3公里以内12.5元,3公里后里程价2.4元/公里,无返空费;调整后, 2公里及2公里以内10元,2公里后里程价2.4元/公里,超过25公里部分,按里程价的30%加收返空费.
(1)请你帮忙计算一下,调价后,若乘客乘坐出租车的行程为8公里,他比以前少付了多少钱(不考虑红灯等因素)?
(2)网上流传“24公里换车”规避返空费,即乘客的行程超过25公里,就在24公里处下车,换乘另一辆出租车.但其实并不是所有行程超过25公里的乘客都需要换车.
例如:①若行程为30公里:不换车,总费用为:
10+23×2.4+5×2.4×130%=80.8元;
换车,总费用为:10+22×2.4+10+4×2.4=82.4元,因此,行程30公里若换车,则费用反而增加2.4元.
②若行程为40公里,不换车,总费用为:
10+23×2.4+15×2.4×130%=112元,若换车,总费用为:10+22×2.4+10+2.4×14=106.4元,则可节约5.6元.
若设行程为x 公里(26<x<48 ),请用含x的式子分别表示出不换车的费用和换车的费用,并帮忙计算一下,行程超过多少公里后换车会就会节约费用(不考虑红灯等因素).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列由四舍五入得到的近似数说法正确的是( )
A.0.720精确到百分位
B.5.078×104精确到千分位
C.3.6万精确到十分位
D.2.90精确到0.01
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,分别以点A和点B为圆心,大于 ![]() AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( ) 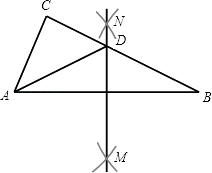
A.7
B.14
C.17
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在纸上画了一条数轴后,折叠纸面,使数轴上表示1的点与表示﹣3的点重合,此时点A与点B也重合,若数轴上A、B两点之间的距离为2018(A在B的左侧),则A点表示的数为( )
A. ﹣1008 B. ﹣1009 C. ﹣1010 D. ﹣1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1 , y1)、B(x2 , y2)在二次函数y=(x﹣1)2+1的图象上,若x1>x2>1,则y1y2(填“>”、“<”或“=”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮? 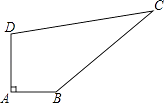
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).
(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
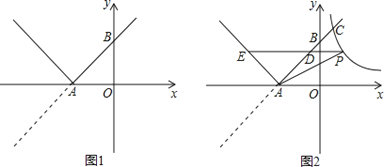
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com