
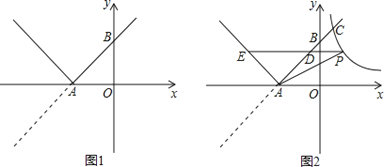
【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).
(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
【答案】(1)①函数的最小值为0;②函数图象的对称轴为直线x=-3;新函数的解析式为y=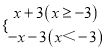 ;(2)△PAD的面积的最大值为
;(2)△PAD的面积的最大值为![]() ;②在点D运动的过程中,四边形PAEC不能为平行四边形.理由见解析.
;②在点D运动的过程中,四边形PAEC不能为平行四边形.理由见解析.
【解析】(1)根据一次函数的性质,结合函数图象可写出新函数的两条性质;求新函数的解析式,可分两种情况进行讨论:①x≥-3时,显然y=x+3;②当x<-3时,利用待定系数法求解;
(2)①先把点C(1,a)代入y=x+3,求出C(1,4),再利用待定系数法求出反比例函数解析式为y=![]() .由点D是线段AC上一动点(不包括端点),可设点D的坐标为(m,m+3),且-3<m<1,那么P(
.由点D是线段AC上一动点(不包括端点),可设点D的坐标为(m,m+3),且-3<m<1,那么P(![]() ,m+3),PD=
,m+3),PD=![]() -m,再根据三角形的面积公式得出△PAD的面积为S=
-m,再根据三角形的面积公式得出△PAD的面积为S=![]() (
(![]() -m)×(m+3)=-
-m)×(m+3)=-![]() m2-
m2-![]() m+2=-
m+2=-![]() (m+
(m+![]() )2+
)2+![]() ,然后利用二次函数的性质即可求解;
,然后利用二次函数的性质即可求解;
②先利用中点坐标公式求出AC的中点D的坐标,再计算DP,DE的长度,如果DP=DE,那么根据对角线互相平分的四边形是平行四边形可得四边形PAEC为平行四边形;如果DP≠DE,那么不是平行四边形.
试题解析:(1)如图1,均是正整数新函数的两条性质:①函数的最小值为0;
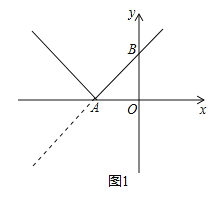
②函数图象的对称轴为直线x=-3;
由题意得A点坐标为(-3,0).分两种情况:
①x≥-3时,显然y=x+3;
②当x<-3时,设其解析式为y=kx+b.
在直线y=x+3中,当x=-4时,y=-1,
则点(-4,-1)关于x轴的对称点为(-4,1).
把(-4,1),(-3,0)代入y=kx+b,
得![]()
解得![]()
∴y=-x-3.
综上所述,新函数的解析式为y=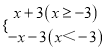 ;
;
(2)如图2,
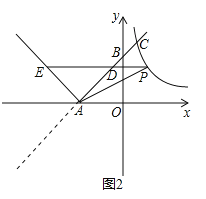
①∵点C(1,a)在直线y=x+3上,
∴a=1+3=4.
∵点C(1,4)在双曲线y=![]() 上,
上,
∴k=1×4=4,y=![]() .
.
∵点D是线段AC上一动点(不包括端点),
∴可设点D的坐标为(m,m+3),且-3<m<1.
∵DP∥x轴,且点P在双曲线上,
∴P(![]() ,m+3),
,m+3),
∴PD=![]() -m,
-m,
∴△PAD的面积为
S=![]() (
(![]() -m)×(m+3)=-
-m)×(m+3)=-![]() m2-
m2-![]() m+2=-
m+2=-![]() (m+
(m+![]() )2+
)2+![]() ,
,
∵a=-![]() <0,
<0,
∴当m=-![]() 时,S有最大值,为
时,S有最大值,为![]() ,
,
又∵-3<-![]() <1,
<1,
∴△PAD的面积的最大值为![]() ;
;
②在点D运动的过程中,四边形PAEC不能为平行四边形.理由如下:
当点D为AC的中点时,其坐标为(-1,2),此时P点的坐标为(2,2),E点的坐标为(-5,2),
∵DP=3,DE=4,
∴EP与AC不能互相平分,
∴四边形PAEC不能为平行四边形.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】一点A从数轴上表示+2的点开始移动,第一次先向左移动1个单位,再向右移动2个单位;第二次先向左移动3个单位,再向右移动4个单位;第三次先向左移动5个单位,再向右移动6个单位……
(1)写出第一次移动后这个点在数轴上表示的数为 ;
(2)写出第二次移动后这个点在数轴上表示的数为 ;
(3)写出第五次移动后这个点在数轴上表示的数为 ;
(4)写出第![]() 次移动结果这个点在数轴上表示的数为 ;
次移动结果这个点在数轴上表示的数为 ;
(5)如果第![]() 次移动后这个点在数轴上表示的数为56,求
次移动后这个点在数轴上表示的数为56,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有三个点A、B、C(如图).请回答:
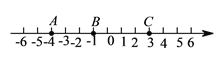
(1)写出数轴上与点B相距5个单位的点M所表示的数为 ;
(2)在数轴上表示:将点C向左移动6个单位到达点D,点A的相反数为点E,并用“<”号把B、D、E三点所表示的数连接起来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B是抛物线y=ax2(a>0)上两点.若点A、B的坐标分别为(3,m)、(4,n),则m_____n.(填“>”、“=”或“<”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用网格画图:
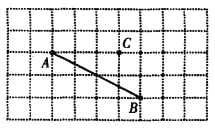
(1)过点C画AB的平行线CD;
(2)过点C画AB的垂线,垂足为E;
(3)线段CE的长度是点C到直线_______的距离;
(4)连接CA、CB,在线段CA、CB、CE中,线段_______最短,理由:_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和
(﹣2,0)之间,其部分图象如下图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知代数式(ax-3)(2x+4)-x2-b化简后,不含x2项和常数项.
(1)求a,b的值;
(2)求(2a+b)2-(a-2b)(a+2b)-3a(a-b)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(﹣3,4)关于y轴的对称点为点B,连接AB,反比例函数y= ![]() (x>0)的图像经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图像上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
(x>0)的图像经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图像上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ. 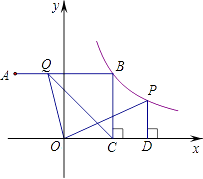
(1)点B的坐标是;k的值为
(2)判断△QDC与△POD的面积是否相等,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com