【题目】观察下列各式及其验证过程： 验证： 
= 
；
验证： = 
= 
= ；
验证： 
= 
；
验证： = 
= 
= ．
（1）按照上述两个等式及其验证过程的基本思路，猜想4 
的变形结果并进行验证；
（2）针对上述各式反映的规律，写出用n（n为任意自然数，且n≥2）表示的等式，并给出证明．
【答案】
（1）解： 
．验证如下：
左边= 
= 
= 
= 
=右边，
故猜想正确
（2）解： 
．证明如下：
左边= 
= 
= 
= 
=右边
【解析】（1）通过观察，不难发现：等式的变形过程利用了二次根式的性质a= 
（a≥0），把根号外的移到根号内；再根据“同分母的分式相加，分母不变，分子相加”这一法则的倒用来进行拆分，同时要注意因式分解进行约分，最后结果中的被开方数是两个数相加，两个加数分别是左边根号外的和根号内的；（2）根据上述变形过程的规律，即可推广到一般．表示左边的式子时，注意根号外的和根号内的分子、分母之间的关系：根号外的和根号内的分子相同，根号内的分子是分母的平方减去1．
【考点精析】利用算数平方根对题目进行判断即可得到答案，需要熟知正数a的正的平方根叫做a的算术平方根；正数和零的算术平方根都只有一个，零的算术平方根是零．
科目：初中数学 来源： 题型：
【题目】如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）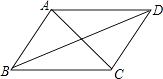 
A.当AB=BC时，它是菱形
B.当AC⊥BD时，它是菱形
C.当∠ABC=90°时，它是矩形
D.当AC=BD时，它是正方形
查看答案和解析>>
科目：初中数学 来源： 题型：
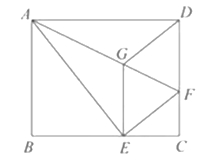
【题目】如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交舡于点G，连接DG．
(1)求证：四边形EFDG是菱形；
(2) 求证： 
；
(3)若AG=6，EG=2
，求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连接CE．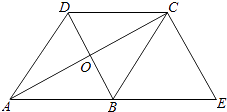 
（1）求证：BD=EC；
（2）若∠E=50°，求∠BAO的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
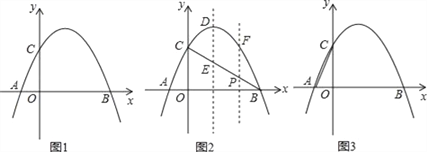
【题目】如图1，抛物线y=﹣x2+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C．
（1）直接写出A、B、C三点的坐标和抛物线的对称轴；
（2）如图2，连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；用含m的代数式表示线段PF的长；并求出当m为何值时，四边形PEDF为平行四边形？
（3）如图3，连接AC，在x轴上是否存在点Q，使△ACQ为等腰三角形，若存在，请求出点Q的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某一线城市对出租车营运价进行了调整，调价前后的收费标准对比如下:调整前,3公里及3公里以内12.5元，3公里后里程价2.4元/公里，无返空费；调整后, 2公里及2公里以内10元，2公里后里程价2.4元/公里，超过25公里部分，按里程价的30%加收返空费．
（1）请你帮忙计算一下，调价后，若乘客乘坐出租车的行程为8公里，他比以前少付了多少钱（不考虑红灯等因素）？
（2）网上流传“24公里换车”规避返空费，即乘客的行程超过25公里，就在24公里处下车，换乘另一辆出租车．但其实并不是所有行程超过25公里的乘客都需要换车．
例如：①若行程为30公里：不换车，总费用为：
10+23×2.4+5×2.4×130%=80.8元；
换车，总费用为：10+22×2.4+10+4×2.4＝82.4元，因此，行程30公里若换车，则费用反而增加2.4元．
②若行程为40公里，不换车，总费用为：
10+23×2.4+15×2.4×130%=112元，若换车，总费用为：10+22×2.4+10+2.4×14＝106.4元，则可节约5.6元．
若设行程为x 公里（26＜x＜48 ），请用含x的式子分别表示出不换车的费用和换车的费用，并帮忙计算一下，行程超过多少公里后换车会就会节约费用（不考虑红灯等因素）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com