Question

【题目】如图1，抛物线y=﹣x2+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C．

（1）直接写出A、B、C三点的坐标和抛物线的对称轴；

（2）如图2，连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；用含m的代数式表示线段PF的长；并求出当m为何值时，四边形PEDF为平行四边形？

（3）如图3，连接AC，在x轴上是否存在点Q，使△ACQ为等腰三角形，若存在，请求出点Q的坐标，若不存在，请说明理由．

Answer 1

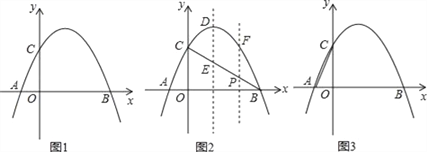
【答案】（1）A（﹣1，0），B（3，0），C（0，3）.对称轴是直线x=1；（2）PF=﹣m2+3m.当m=2时，四边形PEDF为平行四边形；（3）存在，Q1（4，0），Q2（1，0），Q3（﹣1，0），Q4（﹣﹣1，0）．

【解析】试题分析：（1）通过解方程﹣x2+2x+3=0可得A点和B点坐标，再计算自变量为0时的函数值可得到C点坐标，然后利用对称性可确定抛物线的对称轴；（2）先利用待定系数法求出直线BC的函数关系式为y=﹣x+3，再确定E,D点坐标，E（1，2），D（1，4），表示出P（m，﹣m+3），F（m，﹣m2+2m+3），两点纵坐标相减便得PF=﹣m2+3m，接着计算出DE=2，然后利用平行四边形的判定方法，即一组对边平行且相等的四边形是平行四边形，得到﹣m2+3m=2，再解方程求出m即可．（3）分三种情况：QA=QC；CA=CQ；AC=AQ；进行讨论即可求解．

试题解析：（1）当y=0时，﹣x2+2x+3=0，即-（x-3）(x+1)=0,解得x1=﹣1，x2=3，则A（﹣1，0），B（3，0），当x=0时，y=﹣x2+2x+3=3，则C（0，3）；利用A,B点坐标求出抛物线的对称轴是直线x==1；所以A（﹣1，0），B（3，0），C（0，3）.对称轴是直线x=1；（2）设直线BC的函数关系式为y=kx+b，把B（3，0），C（0，3）分别代入得，解得k=﹣1，b=3，∴直线BC的函数关系式为y=﹣x+3，∵对称轴是直线x=1，∴E（1，2），∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴顶点D的坐标为（1，4），当x="m" 时，y=﹣m+3，∴P（m，﹣m+3），F（m，﹣m2+2m+3），∴线段PF=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m，即线段PF=﹣m2+3m，又线段DE=4﹣2=2，∵PF∥DE，∴当PF=ED时，四边形PEDF为平行四边形，即﹣m2+3m=2，解得m1=2，m2=1（不合题意，舍去），∴当m=2时，四边形PEDF为平行四边形；（3）分三种情况：QA=QC；CA=CQ；AC=AQ；进行讨论：设在x轴上存在点Q（x，0），使△ACQ为等腰三角形．分三种情况：①如果QA=QC，那么（x+1）2=x2+32，解得x=4，则点Q1（4，0）；②如果CA=CQ，那么12+32=x2+32，解得x1=1，x2=﹣1（不合题意舍去），则点Q2（1，0）；③如果AC=AQ，那么12+32=（x+1）2，解得x1=﹣1，x2=﹣﹣1，则点Q3（﹣1，0），Q4（﹣﹣1，0）；综上所述存在点Q，使△ACQ为等腰三角形．它的坐标为：Q1（4，0），Q2（1，0），Q3（﹣1，0），Q4（﹣﹣1，0）．