
【题目】(7分)某地政府急灾民之所需,立即组织12辆汽车,将A、B、C三种救灾物资共92吨一次性运往灾区,甲、乙、丙三种车型的汽车分别运载A、B、C三种物资,每辆车按运载量满装物资。假设装运A、B品种物资的车辆数分别为![]() 、
、![]() ,根据下表提供的信息解答下列问题:
,根据下表提供的信息解答下列问题:
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
(1)装运C品种物资车辆数为 辆(用含![]() 与
与![]() 的代数式表示);
的代数式表示);
(2)试求A、B、C三种物资各几吨。
科目:初中数学 来源: 题型:
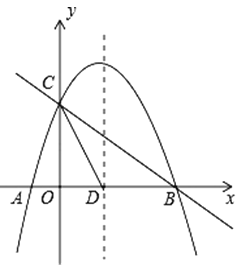
【题目】如图,已知抛物线![]() 与x轴交于A、轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
与x轴交于A、轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图像与一次函数y=x+b的图像交于点 A(1,4)、点B(﹣4,n).
的图像与一次函数y=x+b的图像交于点 A(1,4)、点B(﹣4,n). 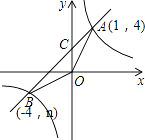
(1)求一次函数和反比例函数的解析式;
(2)若 A1(x1 , y1),A2(x2 , y2),A3(x3 , y3)为双曲线上的三个点,且x1<x2<0<x3 , 请直接写出y1、y2、y3大小关系;
(3)求△OAB的面枳;
(4)直接写出一次函数值大于反比例函数值的自变置x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) 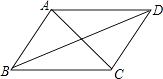
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
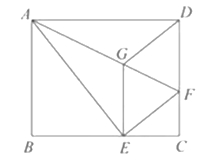
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交舡于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2) 求证: ![]() ;
;
(3)若AG=6,EG=2![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
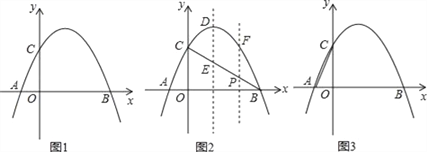
【题目】如图1,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C.
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)如图2,连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;用含m的代数式表示线段PF的长;并求出当m为何值时,四边形PEDF为平行四边形?
(3)如图3,连接AC,在x轴上是否存在点Q,使△ACQ为等腰三角形,若存在,请求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com