
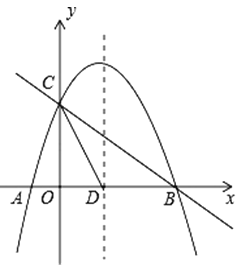
【题目】如图,已知抛物线![]() 与x轴交于A、轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
与x轴交于A、轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2(2)P1(
x+2(2)P1(![]() ,4),P2(
,4),P2(![]() ,
, ![]() ),P3(
),P3(![]() ,﹣
,﹣![]() ).(3)四边形CDBF的面积最大=
).(3)四边形CDBF的面积最大=![]() ,E(2,1)
,E(2,1)
【解析】试题分析:(1)把A(﹣1,0),C(0,2)代入y=﹣![]() x2+mx+n,然后解方程组即可;(2)先确定出抛物线的对称轴x=
x2+mx+n,然后解方程组即可;(2)先确定出抛物线的对称轴x=![]() ,然后△PCD是以CD为腰的等腰三角形分情况讨论即可,(3)求出点B的坐标(4,0),然后求出直线BC的解析式,过点C作CM⊥EF于M,设E(a,﹣
,然后△PCD是以CD为腰的等腰三角形分情况讨论即可,(3)求出点B的坐标(4,0),然后求出直线BC的解析式,过点C作CM⊥EF于M,设E(a,﹣![]() a+2),F(a,﹣
a+2),F(a,﹣![]() a2+
a2+![]() a+2),然后用a表示出四边形CDBF的面积,利用配方法化为顶点式,利用二次函数的性质可解决问题.
a+2),然后用a表示出四边形CDBF的面积,利用配方法化为顶点式,利用二次函数的性质可解决问题.
试题解析:(1)∵抛物线y=﹣![]() x2+mx+n经过A(﹣1,0),C(0,2).
x2+mx+n经过A(﹣1,0),C(0,2).
解得: ![]() ,∴抛物线的解析式为:y=﹣
,∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2 ;
x+2 ;
(2):y=﹣![]() x2+
x2+![]() x+2;∴抛物线的对称轴是x=
x+2;∴抛物线的对称轴是x=![]() .
.
∴OD=![]() .
.
∵C(0,2),∴OC=2.
在Rt△OCD中,由勾股定理,得
CD=![]()
∵△CDP是以CD为腰的等腰三角形,
∴CP1=CP2=CP3=CD.
作CH⊥x轴于H,
∴HP1=HD=2,∴DP1=4.
∴P1(![]() ,4),P2(
,4),P2(![]() ,
, ![]() ),P3(
),P3(![]() ,﹣
,﹣![]() ).
).
(3)当y=0时,0=﹣![]() x2+
x2+![]() x+2
x+2
∴x1=﹣1,x2=4,
∴B(4,0).
设直线BC的解析式为y=kx+b,由图象,得![]() ,解得:
,解得: 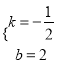 ,
,
∴直线BC的解析式为:y=﹣![]() x+2.
x+2.
如图2,过点C作CM⊥EF于M,
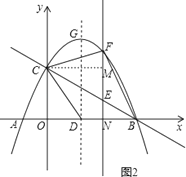
设E(a,﹣ ![]() a+2),F(a,﹣
a+2),F(a,﹣![]() a2+
a2+![]() a+2),
a+2),
∴EF=﹣![]() a2+
a2+![]() a+2﹣(﹣
a+2﹣(﹣![]() a+2)=﹣
a+2)=﹣![]() a2+2a(0≤x≤4).
a2+2a(0≤x≤4).
∵S四边形CDBF=S△BCD+S△CEF+S△BEF=![]() BD
BD![]() OC+
OC+![]() EF
EF![]() CM+
CM+![]() EF
EF![]() BN,
BN,
=![]() +
+![]() a(﹣
a(﹣![]() a2+2a)+
a2+2a)+![]() (4﹣a)(﹣
(4﹣a)(﹣![]() a2+2a),
a2+2a),
=﹣a2+4a+![]() (0≤x≤4).
(0≤x≤4).
=﹣(a﹣2)2+![]()
∴a=2时,S四边形CDBF的面积最大=![]() ,
,
∴E(2,1)


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】据报道,泉州市每年因漏水造成水资源浪费相当严重,每年的漏水量相当于一个小型自来水厂一年的供水量。据不完全统计,全市至少有![]() 个水龙头、
个水龙头、![]() 个抽水马桶存在漏水,若一个关不紧的水龙头一个月漏水
个抽水马桶存在漏水,若一个关不紧的水龙头一个月漏水![]() ,一个抽水马桶一个月漏水
,一个抽水马桶一个月漏水![]() ,那么泉州市一个月因漏水而造成水浪费是多少
,那么泉州市一个月因漏水而造成水浪费是多少![]() ?(结果精确到千位)
?(结果精确到千位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一:
(A)计时制:0.05元/分;
(B)包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为![]() 分,请你用含
分,请你用含![]() 的代数式分别写出两种收费方式下该用户应该支付的费用;
的代数式分别写出两种收费方式下该用户应该支付的费用;
(2)如果某用户一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某地政府急灾民之所需,立即组织12辆汽车,将A、B、C三种救灾物资共92吨一次性运往灾区,甲、乙、丙三种车型的汽车分别运载A、B、C三种物资,每辆车按运载量满装物资。假设装运A、B品种物资的车辆数分别为![]() 、
、![]() ,根据下表提供的信息解答下列问题:
,根据下表提供的信息解答下列问题:
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
(1)装运C品种物资车辆数为 辆(用含![]() 与
与![]() 的代数式表示);
的代数式表示);
(2)试求A、B、C三种物资各几吨。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com