
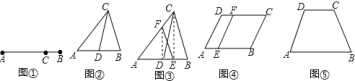
【题目】如图①所示,点![]() 将线段
将线段![]() 分成两部分,如果
分成两部分,如果![]() ,那么称点
,那么称点![]() 为线段
为线段![]() 的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线将一个面积为
的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线将一个面积为![]() 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为![]() ,
,![]() ,如果
,如果![]() ,那么称直线为该图形的黄金分割线.
,那么称直线为该图形的黄金分割线.
问题探究:
(1)研究小组猜想:在![]() 中,若点
中,若点![]() 为
为![]() 上的黄金分割点,如图②,则直线
上的黄金分割点,如图②,则直线![]() 是
是![]() 的黄金分割线,你认为呢?为什么?
的黄金分割线,你认为呢?为什么?
(2)研究小组在进一步探究中发现:过点![]() 任作一条直线交
任作一条直线交![]() 于点
于点![]() ,再过点
,再过点![]() 作直线
作直线![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 如图③,则直线
如图③,则直线![]() 也是
也是![]() 的黄金分割线,请你说明理由.
的黄金分割线,请你说明理由.
(3)如图④,点![]() 是平行四边形
是平行四边形![]() 的边
的边![]() 的黄金分割点,过点
的黄金分割点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,显然直线
,显然直线![]() 是平行四边形的黄金分割线,请你画一条平行四边形
是平行四边形的黄金分割线,请你画一条平行四边形![]() 的黄金分割线,使它不经过四边形
的黄金分割线,使它不经过四边形![]() 各边黄金分割点.
各边黄金分割点.
(4)如图⑤等腰梯形![]() ,请你画出它的一条黄金分割线,使它不经过各边的黄金分割点.
,请你画出它的一条黄金分割线,使它不经过各边的黄金分割点.
【答案】(1)直线![]() 是
是![]() 的黄金分割线,理由见解析;(2)直线
的黄金分割线,理由见解析;(2)直线![]() 也是
也是![]() 的黄金分割线,理由见解析;(3)直线
的黄金分割线,理由见解析;(3)直线![]() 就是平行四边形
就是平行四边形![]() 的黄金分割线;(4)直线
的黄金分割线;(4)直线![]() 就是等腰梯形
就是等腰梯形![]() 的黄金分割线.
的黄金分割线.
【解析】
(1)若点D为AB边上的黄金分割点,则有![]() =
=![]() .如果设△ABC的边AB上的高为h,根据三角形的面积公式,易得
.如果设△ABC的边AB上的高为h,根据三角形的面积公式,易得![]() =
=![]() ,
,![]() =
=![]() ,即有
,即有![]() =
=![]() ,根据图形的黄金分割线的定义即可判断;
,根据图形的黄金分割线的定义即可判断;
(2)由于直线CD是△ABC的黄金分割线,所以![]() =
=![]() .要想说明直线EF也是△ABC的黄金分割线,只需证明
.要想说明直线EF也是△ABC的黄金分割线,只需证明![]() =
=![]() ,即证S△ADC=S△AEF,S△BDC=S四边形BEFC即可.因为DF∥CE,所以△DFC和△DFE的公共边DF上的高也相等,所以有S△DFC=S△DFE,所以S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF,S△BDC=S四边形BEFC.
,即证S△ADC=S△AEF,S△BDC=S四边形BEFC即可.因为DF∥CE,所以△DFC和△DFE的公共边DF上的高也相等,所以有S△DFC=S△DFE,所以S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF,S△BDC=S四边形BEFC.
(3)根据黄金分割线的定义即可作出.本题答案不唯一,作法有无数种.
(4) 分别作出AB、CD的黄金分割点E、F,在FC上取一点N,连接EN,再过点F作FM//NE交AB于点M,连接MN即可.
解:(1)设![]() 边
边![]() 上的高为
上的高为![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 为
为![]() 上的黄金分割点,
上的黄金分割点,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 是
是![]() 的黄金分割线;
的黄金分割线;
(2)∵![]() ,
,
∴![]() 和
和![]() 的公共边
的公共边![]() 上的高也相等,
上的高也相等,
∴![]() ,
,
如图③,设直线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,

∵![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴直线![]() 也是
也是![]() 的黄金分割线;
的黄金分割线;
(3)如图④,在![]() 上取一点
上取一点![]() ,连接
,连接![]() ,再过点
,再过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
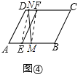
则直线![]() 就是平行四边形
就是平行四边形![]() 的黄金分割线;
的黄金分割线;
(4)如图⑤,分别作出![]() 、
、![]() 的黄金分割点
的黄金分割点![]() 、
、![]() ,在
,在![]() 上取一点
上取一点![]() ,连接
,连接![]() ,再过点
,再过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,
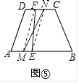
则直线![]() 就是等腰梯形
就是等腰梯形![]() 的黄金分割线.
的黄金分割线.
故答案为:(1)直线![]() 是
是![]() 的黄金分割线,理由见解析;(2)直线
的黄金分割线,理由见解析;(2)直线![]() 也是
也是![]() 的黄金分割线,理由见解析;(3)直线
的黄金分割线,理由见解析;(3)直线![]() 就是平行四边形
就是平行四边形![]() 的黄金分割线;(4)直线
的黄金分割线;(4)直线![]() 就是等腰梯形
就是等腰梯形![]() 的黄金分割线.
的黄金分割线.


科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:
当![]() ,
,![]() 时,
时,
![]() ,
,
![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
请利用上述结论解决以下问题:
(1)当![]() 时,
时,![]() 的最小值为__________.
的最小值为__________.
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
(3)请解答以下问题:
如图所示,某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙足够长),另外三边用篱笆围成,设垂直于墙的一边长为![]() 米.若要围成面积为200平方米的花圃,需要用的篱笆最少是__________米.
米.若要围成面积为200平方米的花圃,需要用的篱笆最少是__________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期初,某校为迎接中华人民共和国成立七十周年,开展了以“不忘初心,缅怀革命先烈,奋斗新时代“为主题的读书活动.德育处对八年级学生九月份“阅读该主题相关书籍的读书量”( 下面简称:“读书量”)进行了随机抽样调查,并对所有随机抽取学生的“读书量”(单位:本)进行了统计,绘制了两幅不完整的统计图(如图所示).
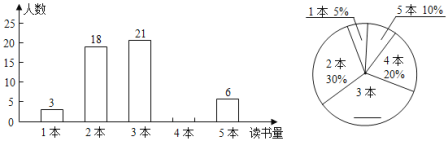
(1)请补全两幅统计图;本次所抽取学生九月份“读书量“的众数为 本;
(2)求本次所抽取学生九月份“读书量”的平均数;
(3)已知该校八年级有500名学生,请你估计该校八年级学生中,九月份“读书量“为5本的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
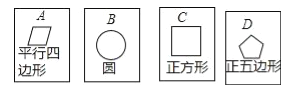
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
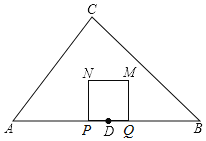
【题目】如图,在△ABC中,AB=14,∠B=45°,tanA=![]() ,点D为AB中点.动点P从点D出发,沿DA方向以每秒1个单位长度的速度向终点A运动,点P关于点D对称点为点Q,以PQ为边向上作正方形PQMN.设点P的运动时间为t秒.
,点D为AB中点.动点P从点D出发,沿DA方向以每秒1个单位长度的速度向终点A运动,点P关于点D对称点为点Q,以PQ为边向上作正方形PQMN.设点P的运动时间为t秒.
(1)当t=______秒时,点N落在AC边上.
(2)设正方形PQMN与△ABC重叠部分面积为S,当点N在△ABC内部时,求S关于t的函数关系式.
(3)当矩形PQMN的对角线所在直线将△ABC的分为面积相等的两部分时,直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com