
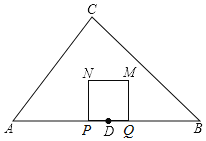
【题目】如图,在△ABC中,AB=14,∠B=45°,tanA=![]() ,点D为AB中点.动点P从点D出发,沿DA方向以每秒1个单位长度的速度向终点A运动,点P关于点D对称点为点Q,以PQ为边向上作正方形PQMN.设点P的运动时间为t秒.
,点D为AB中点.动点P从点D出发,沿DA方向以每秒1个单位长度的速度向终点A运动,点P关于点D对称点为点Q,以PQ为边向上作正方形PQMN.设点P的运动时间为t秒.
(1)当t=______秒时,点N落在AC边上.
(2)设正方形PQMN与△ABC重叠部分面积为S,当点N在△ABC内部时,求S关于t的函数关系式.
(3)当矩形PQMN的对角线所在直线将△ABC的分为面积相等的两部分时,直接写出t的值.
【答案】(1)![]() ;(2)S=
;(2)S= ;(3)t的值为4
;(3)t的值为4![]() -7或7
-7或7![]() -7
-7
【解析】
(1)作CG⊥AB,由∠B=45°可设BG=CG=h,AG=14-h,根据tanA=![]() 求得h=8,再证△APN∽△AGC得
求得h=8,再证△APN∽△AGC得![]() ,据此求解可得;(2)分点M在△ABC内部和外部两种情况:点M在△ABC内部时,重叠部分面积即为正方形的面积;点M在△ABC外部时,重叠部分面积=正方形PQMN的面积-△EMF的面积,据此求解;(3)分直线PM和直线QN将△ABC面积平分的两种情况分别求解可得.
,据此求解可得;(2)分点M在△ABC内部和外部两种情况:点M在△ABC内部时,重叠部分面积即为正方形的面积;点M在△ABC外部时,重叠部分面积=正方形PQMN的面积-△EMF的面积,据此求解;(3)分直线PM和直线QN将△ABC面积平分的两种情况分别求解可得.
(1)如图1,作CG⊥AB于点G,

设BG=h,∵∠B=45°,AB=14,
∴CG=BG=h,AG=14-h,
∵tanA=![]() ,即
,即![]() ,
,
解得:h=8,
则AG=6,
∵DP=DQ=t,
∴PN=PQ=2t,
由PN∥CG知△APN∽△AGC,
∴![]() ,即
,即![]() ,
,
解得:t=![]() ,
,
故答案为:![]() .
.
(2)①如图2,

∵四边形PQMN是正方形,
∴∠BQM=90°,
∵∠B=45°,
∴BQ=MQ,即7-t=2t,
解得t=![]() ,
,
故当0<t≤![]() 时,S=(2t)2=4t2;
时,S=(2t)2=4t2;
②如图3,

∵∠BQF=90°,∠B=45°,
∴BQ=FQ=7-t,∠BFQ=∠MFE=45°,
则MF=MQ-QF=3t-7,
∵∠M=90°,
∴ME=MF=3t-7,
则S=(2t)2-![]() ×(3t-7)2=-
×(3t-7)2=-![]() t2+21t-
t2+21t-![]() (
(![]() <t<
<t<![]() );
);
综上,S= .
.
(3)S△ABC=![]() ABCG=
ABCG=![]() ×14×8=56,
×14×8=56,
①如图4,作HR⊥AB于点R,
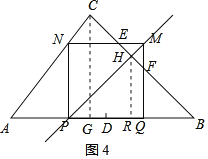
∵四边形PQMN为正方形,且PM为对角线,
∴∠HPB=∠B=45°,
∴HR=![]() PB=
PB=![]() ×(14-7+t)=
×(14-7+t)=![]() ,
,
∵PM将△ABC面积平分,
∴S△PBH=![]() S△ABC,
S△ABC,
则![]() (7+t)
(7+t)![]() =
=![]() ×56,
×56,
解得t=-7+4![]() (负值舍去);
(负值舍去);
②如图5,作KT⊥AB于T,
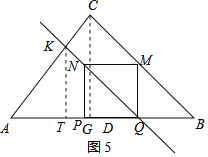
设KT=4m,由tanA=![]() 知AT=3m,
知AT=3m,
∵∠KQT=45°,
∴KT=QT=4m,
则AQ=3m+4m=7m,
又AQ=14-(7-t)=7+t,
则7m=7+t,
∴m=![]() ,
,
∵直线NQ将△ABC面积平分,
∴S△AKQ=![]() S△ABC,即
S△ABC,即![]() ×7m×4m=
×7m×4m=![]() ×56,
×56,
整理,得:m2=2,
则(![]() span>)2=2,
span>)2=2,
解得:t=-7+7![]() (负值舍去),
(负值舍去),
综上,t的值为4![]() -7或7
-7或7![]() -7.
-7.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图①所示,点![]() 将线段
将线段![]() 分成两部分,如果
分成两部分,如果![]() ,那么称点
,那么称点![]() 为线段
为线段![]() 的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线将一个面积为
的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线将一个面积为![]() 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为![]() ,
,![]() ,如果
,如果![]() ,那么称直线为该图形的黄金分割线.
,那么称直线为该图形的黄金分割线.
问题探究:
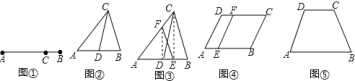
(1)研究小组猜想:在![]() 中,若点
中,若点![]() 为
为![]() 上的黄金分割点,如图②,则直线
上的黄金分割点,如图②,则直线![]() 是
是![]() 的黄金分割线,你认为呢?为什么?
的黄金分割线,你认为呢?为什么?
(2)研究小组在进一步探究中发现:过点![]() 任作一条直线交
任作一条直线交![]() 于点
于点![]() ,再过点
,再过点![]() 作直线
作直线![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() 如图③,则直线
如图③,则直线![]() 也是
也是![]() 的黄金分割线,请你说明理由.
的黄金分割线,请你说明理由.
(3)如图④,点![]() 是平行四边形
是平行四边形![]() 的边
的边![]() 的黄金分割点,过点
的黄金分割点,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,显然直线
,显然直线![]() 是平行四边形的黄金分割线,请你画一条平行四边形
是平行四边形的黄金分割线,请你画一条平行四边形![]() 的黄金分割线,使它不经过四边形
的黄金分割线,使它不经过四边形![]() 各边黄金分割点.
各边黄金分割点.
(4)如图⑤等腰梯形![]() ,请你画出它的一条黄金分割线,使它不经过各边的黄金分割点.
,请你画出它的一条黄金分割线,使它不经过各边的黄金分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
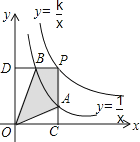
【题目】反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴,交y=
的图象上,PC⊥x轴,交y=![]() 的图象于点A,PD⊥y轴,交y=
的图象于点A,PD⊥y轴,交y=![]() 的图象于点B.当点P在y=
的图象于点B.当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
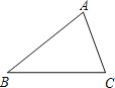
【题目】下面是小芸设计的“作三角形一边上的中线”的尺规作图过程.
已知:△ABC.
求作:BC边上的中线AD.
作法:
(1)分别以点B,C为圆心,AC,AB长为半径画弧,
两弧相交于P点;
(2)作直线AP,AP与BC交于D点.
线段AD就是所求作的BC边上的中线.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:连接BP,CP,
∵AB=CP,AC=______,
∴四边形ABPC是平行四边形,(______)(填推理的依据)
∴BD=DC,(______)(填推理的依据)
即线段AD是BC边上的中线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于平面直角坐标系xOy中的点P(a,b)和直线y=ax+b,我们称点P((a,b)是直线y=ax+b的关联点,直线y=ax+b是点P(a,b)的关联直线.特别地,当a=0时,直线y=b(b为常数)的关联点为P(0,b).
如图,已知点A(-2,-2),B(4,-2),C(1,4).
(1)点A的关联直线的解析式为______;
直线AB的关联点的坐标为______;
(2)设直线AC的关联点为点D,直线BC的关联点为点E,点P在y轴上,且S△DEP=2,求点P的坐标.
(3)点M(m,n)是折线段AC→CB(包含端点A,B)上的一个动点.直线l是点M的关联直线,当直线l与△ABC恰有两个公共点时,直接写出m的取值范围.
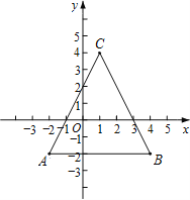
查看答案和解析>>
科目:初中数学 来源: 题型:
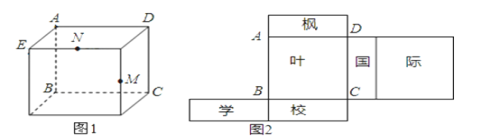
【题目】如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)面“学”的对面是面什么?
(2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究: 如图,直线![]() 的表达式为
的表达式为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的表达式;
的表达式;
(3)求![]() 的值;
的值;
(4)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() ?若存在,请直接写出点
?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com