
【题目】若整数a能被整数b整除,则一定存在整数n,使得![]() =n,即a=bn,例如:若整数a能被整数7整除,则一定存在整数n,使得
=n,即a=bn,例如:若整数a能被整数7整除,则一定存在整数n,使得![]() =n,即a=7n.
=n,即a=7n.
(1)将一个多位自然数分解为个位与个位之前的数,让个位之前的数减去个位数的两倍,若所得之差能被7整除,则原多位自然数一定能被7整除.例如:将数字1078分解为8和107,107﹣8×2=91,因为91能被7整除,所以1078能被7整除,请你证明任意一个三位数都满足上述规律.
(2)若将一个多位自然数分解为个位与个位之前的数,让个位之前的数加上个位数的k(k为正整数,1≤k≤15)倍,所得之和能被13整除,求当k为何值时使得原多位自然数一定能被13整除.
【答案】(1)见解析;(2)见解析
【解析】
试题分析:(1)根据题意设![]() ﹣2c=10a+b能被7整除,再假设
﹣2c=10a+b能被7整除,再假设![]() ﹣2c=7n( n为自然数 ),则10n+b=7n,进而表示出
﹣2c=7n( n为自然数 ),则10n+b=7n,进而表示出![]() ,即可得出答案;
,即可得出答案;
(2)首先设m+kn=13a,10m+n=13b,则原多位数为10m+n,进而得出b与a,k的关系,进而得出答案.
解:(1)设任意一个三位数为![]() (均为自然数且),
(均为自然数且),
依题意假设 ![]() ﹣2c=10a+b能被7整除,
﹣2c=10a+b能被7整除,
不妨设![]() ﹣2c=7n( n为自然数 ),则10n+b=7n,
﹣2c=7n( n为自然数 ),则10n+b=7n,
![]() =100a+10b+c=10(10a+b)+c=10(7n+2c)+c=7(10n+3c),
=100a+10b+c=10(10a+b)+c=10(7n+2c)+c=7(10n+3c),
所以 ![]() 能被7整除;
能被7整除;
(2)以下出现的字母均为自然数,设个位之前及个位数分别为m、n,
依题意不妨设m+kn=13a,
则原多位数为10m+n,
依题意不妨设10m+n=13b,
联立可得:b=10a﹣![]() (10k﹣1),
(10k﹣1),
则10k﹣1为13倍数,分别将 k=1、2、3、4、5…15代入可知,只有k=4 时符合条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
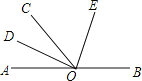
(1)若∠AOC=50°,求出∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点A在y轴正半轴上,点B的坐标为(0,﹣3),反比例函数y=﹣![]() 的图象经过点C.
的图象经过点C.
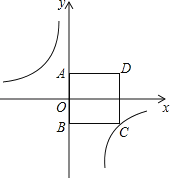
(1)求点C的坐标;
(2)若点P是反比例函数图象上的一点且S△PAD=S正方形ABCD;求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
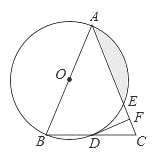
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com