练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】等边三角形的边长为a，则它的周长为_____．

    【答案】3a

    【解析】等边三角形的边长为a，进而求出它的周长．

    解：因为等边三角形的三边相等，而等边三角形的边长为a，所以它的周长为3a．

    故答案为3a．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AD=CD，∠DAB=∠ACB=90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．

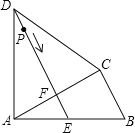
    （1）求证：ABCF=CBCD；

    （2）已知AB=15，BC=9，P是射线DE上的动点，设DP=x（x＞0），四边形BCDP的面积为y．

    ①求y关于x的函数关系式；

    ②当PB+PC最小时，求x，y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A(a，1)与点A′(5，b)关于坐标原点对称，则实数a、b的值是（ ）

    A．a＝5，b＝1 B．a＝－5，b＝1

    C．a＝5，b＝－1 D．a＝－5，b＝－1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点A（﹣2，3）关于y轴对称的点A′的坐标是（ ）

    A.(－2,6) B.(2,3) C.(－2，－3) D.(2，－3)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是（ ）

    A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系中有两点M（a，b），N（c，d），规定（a，b）⊕（c，d）=（a+c，b+d），则称点Q（a+c，b+d）为M，N的“和点”．若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形，则称这个四边形为“和点四边形”，现有点A（2，5），B（﹣1，3），若以O，A，B，C四点为顶点的四边形是“和点四边形”，则点C的坐标是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，OM平分∠AOB，MC∥OB，MD⊥OB于D，若∠OMD=75°，OC=8，则MD的长为（ ）

    A．2 B．3 C．4 D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题：①负数没有立方根，②一个实数的立方根不是正数就是负数，③一个正数或负数的立方根与这个数的符号一致，④如果一个数的立方根等于它本身，那么它一定是1或0.其中正确的是( )

    A、1 B、2 C、3 D、4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若整数a能被整数b整除，则一定存在整数n，使得=n，即a=bn，例如：若整数a能被整数7整除，则一定存在整数n，使得=n，即a=7n．

    （1）将一个多位自然数分解为个位与个位之前的数，让个位之前的数减去个位数的两倍，若所得之差能被7整除，则原多位自然数一定能被7整除．例如：将数字1078分解为8和107，107﹣8×2=91，因为91能被7整除，所以1078能被7整除，请你证明任意一个三位数都满足上述规律．

    （2）若将一个多位自然数分解为个位与个位之前的数，让个位之前的数加上个位数的k（k为正整数，1≤k≤15）倍，所得之和能被13整除，求当k为何值时使得原多位自然数一定能被13整除．

    查看答案和解析>>

    同步练习册答案