
【题目】如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
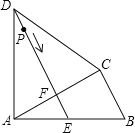
(1)求证:ABCF=CBCD;
(2)已知AB=15,BC=9,P是射线DE上的动点,设DP=x(x>0),四边形BCDP的面积为y.
①求y关于x的函数关系式;
②当PB+PC最小时,求x,y的值.
【答案】(1)见解析;(2)①y=![]() (x+9)×6=3x+27(x>0);②x=
(x+9)×6=3x+27(x>0);②x=![]() ,此时y=
,此时y=![]() .
.
【解析】
试题分析:(1)首先证得△DCF∽△ABC,利用相似三角形的性质可得结论;
(2)①由勾股定理可得BC的长,利用梯形的面积公式可得结果;②首先由垂直平分线的性质可得点C关于直线DE的对称点是点A,PB+PC=PB+PA,故只要求PB+PA最小即可,因为当P、A、B三点共线时PB+PA最小,由中位线的性质可得EF=![]() ,由(1)知CF:BC=CD:AB,可得CD,即得AD,在Rt△ADF中,由勾股定理可得DF,易得DE,即得x,代入①可得y.
,由(1)知CF:BC=CD:AB,可得CD,即得AD,在Rt△ADF中,由勾股定理可得DF,易得DE,即得x,代入①可得y.
(1)证明:如图1,∵AD=CD,DE⊥AC,
∴DE垂直平分AC,
∴AF=CF,∠DFA=∠DFC=90°,∠DAF=∠DCF,
∵∠DAB=∠DAF+∠CAB=90°,∠CAB+∠B=90°,
∴∠DCF=∠DAF=∠B,
在Rt△DCF和Rt△ABC中,∠DFC=∠ACB=90°,∠DCF=∠B,
∴△DCF∽△ABC,
∴![]() ,
,
∴ABCF=CBCD;
(2)解:①∵AB=15,BC=9,∠ACB=90°,
∴AC=![]() =
=![]() =12,
=12,
∴CF=AF=6,
∴y=![]() (x+9)×6=3x+27(x>0);
(x+9)×6=3x+27(x>0);
②由(1)知点C关于直线DE的对称点是点A,
∴PB+PC=PB+PA,故只要求PB+PA最小,显然当P、A、B三点共线时PB+PA最小,
此时DP=DE,PB+PA=AB,
∵EF∥BC,∴EF=![]() ,
,
∵CF:BC=CD:AB,即6:9=CD:15,
∴CD=10=AD,
Rt△ADF中,AD=10,AF=6,
∴DF=8,
∴DE=DF+EF=8+![]() =
=![]() ,
,
∴x=![]() ,此时y=
,此时y=![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如果A和B都是5次多项式,则下面说法正确的是()
A. A-B一定是多项式 B. A-B是次数不低于5的整式
C. A+B一定是单项式 D. A+B是次数不高于5的整式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题:
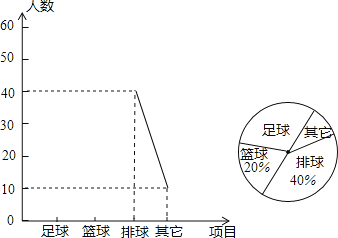
(1)在这次调查中,一共调查 名学生;
(2)在扇形统计图中,“足球”所在扇形圆心角 度;
(3)将折线统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上出了一道解方程的题![]() =1﹣
=1﹣![]() ,小明马上举起了手,要求到黑板上去做,他是这样做的:
,小明马上举起了手,要求到黑板上去做,他是这样做的:
4(2x﹣1)=1﹣3(x+2)①
8x﹣4=1﹣3x﹣6 ②
8x+3x=1﹣6+4 ③
11x=﹣1 ④
![]() ⑤
⑤
老师说:小明解一元一次方程的一般步骤都掌握了,但解题时有一步做错了,请你指出他错在第 步(填编号),错误的原因是 ;然后,你自己细心地解下列方程:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com