
【题目】某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题:
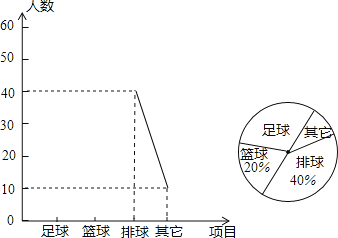
(1)在这次调查中,一共调查 名学生;
(2)在扇形统计图中,“足球”所在扇形圆心角 度;
(3)将折线统计图补充完整.
【答案】(1)100,(2)108.(3)见解析
【解析】
试题分析:(1)根据爱好“排球”有40人,占被调查人数的40%列式计算可得总人数;
(2)先求出“其他”所占百分比,再用1减去其他三项百分比可得足球占总人数的百分比,利用百分比可得扇形圆心角度数;
(3)根据足球的百分比及总人数可得足球人数,用总人数减去足球、排球、其他三项人数可得篮球的人数,即可补全图形.
解:(1)根据题意,知爱好“排球”的有40人,占被调查人数的40%,
故被调查人数为:40÷40%=100(人);
(2)“其他”项目占被调查人数百分比为:![]() ×100%=10%,
×100%=10%,
则“足球”项目人数占被调查人数的百分比为:1﹣(20%+40%+10%)=30%,
则在扇形统计图中,“足球”所在扇形圆心角为:360°×30%=108°;
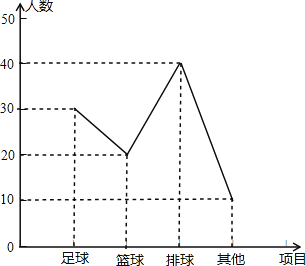
(3)爱好“足球”人数为:100×30%=30人,
爱好“篮球”人数为:100﹣30﹣40﹣10=20人,补全折线统计图如下:
故答案为:(1)100,(2)108.


科目:初中数学 来源: 题型:
【题目】粗心的小红在计算n边形的内角和时,少加了一个内角,求得的内角和是2040°,则这个多边形的边数n和这个内角分别是( )
A.11和60° B.11和120° C.12和60° D.14和120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )
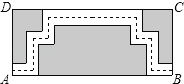
A.100米 B.99米 C.98米 D.74米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E,A在直线DC同侧,连接AE.求证:

(1)△AEC≌BDC;
(2)AE∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
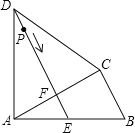
(1)求证:ABCF=CBCD;
(2)已知AB=15,BC=9,P是射线DE上的动点,设DP=x(x>0),四边形BCDP的面积为y.
①求y关于x的函数关系式;
②当PB+PC最小时,求x,y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
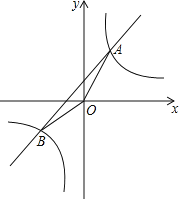
(1)求一次函数与反比例函数的解析式;
(2)求△ABO的面积;
(3)根据所给条件,请直接写出不等式kx+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
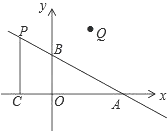
(1)当b=3时,
①求直线AB的解析式;
②若QO=QA,求P点的坐标.
(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每组数分别表示三根木棒的长度,将它们首尾连接后,能摆成三角形的一组是( )
A.1,2,6 B.2,2,4 C.1,2,3 D.2,3,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com