
【题目】如图,∠1=65°,∠2=50°,∠3=115°,EG平分∠NEF,
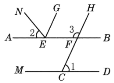
试说明:(1)AB∥CD;
(2)EG∥FH的理由.
【答案】(1)见解析;(2)理由见解析.
【解析】
(1)已知∠3的度数,根据邻补角定义可以求出∠HFB的度数,与∠1的度数相等,根据同位角相等两直线平行即可得AB∥CD;
(2)根据角平分线定义可以得出∠GEF=∠NEG,根据平角定义即可求出∠GEF的度数即可得出EG∥FH.
证明:(1)∵∠3=115°,∠3+∠HFB=180°,
∴∠HFB=180°-115°=65°,
∴∠1=∠HFB,
∴AB∥CD;
(2)∵EG平分∠NEF,
∴∠GEF=∠NEG,∠2=50°,
∵∠2+∠NEG+∠GEF=180°,
∴∠GEF=![]() (180°-∠2)=
(180°-∠2)= ![]() (180°-50°)=65°.
(180°-50°)=65°.
即∠GEF=∠HFB=65°,
∴EG∥FH.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
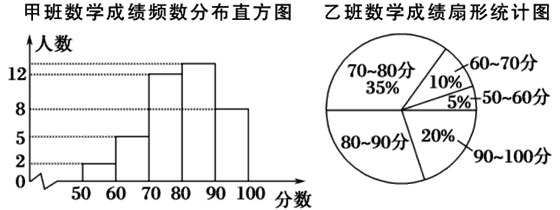
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论: ①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若 ![]() =
= ![]() ,则3S△EDH=13S△DHC , 其中结论正确的有 .
,则3S△EDH=13S△DHC , 其中结论正确的有 . 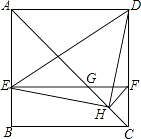
查看答案和解析>>
科目:初中数学 来源: 题型:
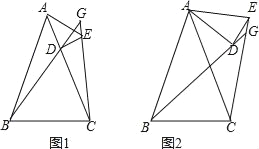
【题目】已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,
(1)如图1,点D在AC上,求证:∠BGC=∠BAC;
(2)如图2,当点D不在AC上,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )
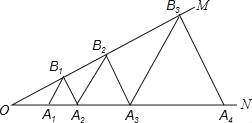
A. 32 B. 64 C. 128 D. 256
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
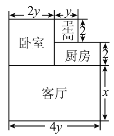
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:
(1)用含x的代数式表示地面总面积;
(2)当x=4,y=2时,铺1 m2地砖的平均费用为30元,那么铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过15吨(含15吨)时,每吨按政府补贴优惠价收费;每月超过15吨时,超过部分每吨按市场调节价收费.小明家1月份用水23吨,交水费35元,2月份用水19吨,交水费25元.
(1)求每吨水的政府补贴优惠价与市场调节价分别是多少;
(2)小明家3月份用水24吨,他家应交水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com