
【题目】已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,
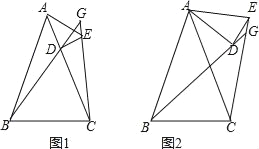
(1)如图1,点D在AC上,求证:∠BGC=∠BAC;
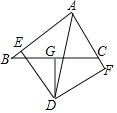
(2)如图2,当点D不在AC上,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】
试题此题考查全等三角形的判定和性质,关键是证明△AEC≌△ADB.
(1)证△ABD和△ACE全等得出∠ABD=∠ACE,又∠ADB=∠GDC,证明∠BGC=∠BAC即可;
(2)先证△AEC≌△ADB,则有∠ABG=∠ACE,再加上对顶角相等;得出∠BGC=∠BAC即可.
试题解析:证明:(1)在△ABD和△ACE中,
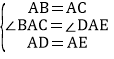 ,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠ADB=∠GDC,
∴∠BGC=∠BAC;
(2)成立,理由如下:
在△AEC与△ADB中,
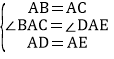 ,
,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,
∵∠ADB=∠GDC,
∴∠BGC=∠BAC.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】联想与探索:
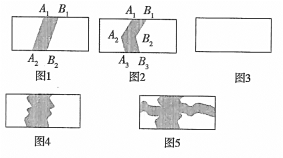
如图1,将线段A1A2本向右平移1个单位长度至B1B2,得到封闭图形A1A2B2B1(即阴影部分),在图2中,将折线A1A2A3向右平移1个单位长度至B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图3中,请你类似地画一条有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形水平方向长均为a,竖直方向长均为b) :S1= ,S2= ,S3= ;
(3)如图4,在一块长方形草地上,有一条弯曲的小路(小路任何地方的水平宽度都是2个单位长度,长方形水平方向长为a,竖直方向长为b),则空白部分表示的草地面积是多少?
(4)如图5,若在(3)中的草地上又有一条横向的曲小路(小路任何地方的宽度都是1个单位长度),则空白部分表示的草地面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是______ .
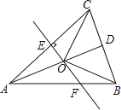
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=130°,则∠A的度数是( )
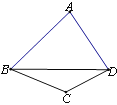
A.60° B.70° C.80° D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD各顶点分别为A(-2,2),B(-2,-1),C(3,-1),D(3,2),如果长方A'B'C'D'先向右平移1个单位长度,再向下平移2个单位长度,恰能与长方形ABCD完全重合.
(1)求长方形A'B'C'D'各顶点的坐标;
(2)如果线段AB与线段B'C'交于点E,线段AD与线段C'D'交于点F,求点E,F的坐标.
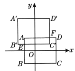
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE. 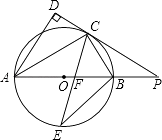
(1)求证:AC平分∠DAB;
(2)探究线段PC,PF之间的大小关系,并加以证明;
(3)若tan∠PCB= ![]() ,BE=
,BE= ![]() ,求PF的长.
,求PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com