
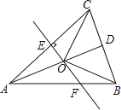
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是______ .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD, 
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.
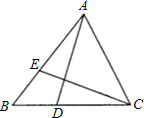
(1)给出下列四个条件:①AD=CE ②AE=CD ③∠BAC=∠BCA ④∠ADB=∠CEB请你从中选出一个能使△ADB≌△CEB的条件,并给出证明;
你选出的条件是
证明:
(2)在(1)中所给出的条件中,能使△ADB≌△CEB的还有哪些?直接在题后横线上写出满足题意的条件序号:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离. 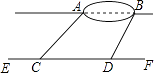
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
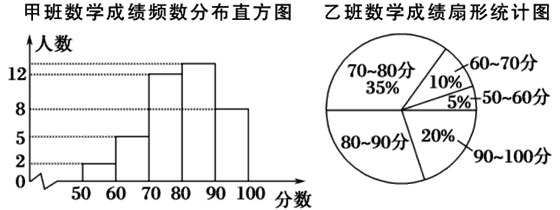
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①若x=0,则x2﹣2x=0;②若 ![]() =
= ![]() ,则a=b;③矩形既是轴对称图形又是中心对称图形;④圆内接四边形的对角一定相等.其中原命题与逆命题均为真命题的个数是( )
,则a=b;③矩形既是轴对称图形又是中心对称图形;④圆内接四边形的对角一定相等.其中原命题与逆命题均为真命题的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
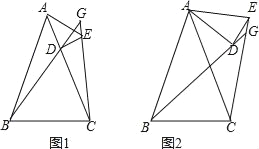
【题目】已知AB=AC,AD=AE,∠BAC=∠DAE,直线BD、CE交于点G,
(1)如图1,点D在AC上,求证:∠BGC=∠BAC;
(2)如图2,当点D不在AC上,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°. 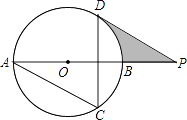
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com