
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】联想与探索:
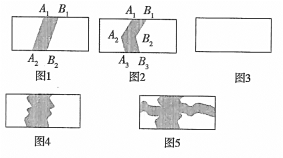
如图1,将线段A1A2本向右平移1个单位长度至B1B2,得到封闭图形A1A2B2B1(即阴影部分),在图2中,将折线A1A2A3向右平移1个单位长度至B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图3中,请你类似地画一条有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形水平方向长均为a,竖直方向长均为b) :S1= ,S2= ,S3= ;
(3)如图4,在一块长方形草地上,有一条弯曲的小路(小路任何地方的水平宽度都是2个单位长度,长方形水平方向长为a,竖直方向长为b),则空白部分表示的草地面积是多少?
(4)如图5,若在(3)中的草地上又有一条横向的曲小路(小路任何地方的宽度都是1个单位长度),则空白部分表示的草地面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆O1、圆O2的半径不相等,圆O1的半径长为3,若圆O2上的点A满足AO1=3,则圆O1与圆O2的位置关系是( )
A.相交或相切
B.相切或相离
C.相交或内含
D.相切或内含
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=2,∠BA C=75°,∠ACB= 60°,高BE与AD相交于点H,则DH的长为
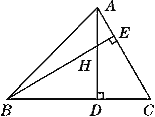
A. 2 B. 1.5 C. 1 D. 0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
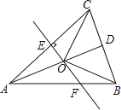
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE. 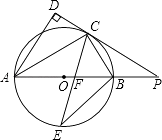
(1)求证:AC平分∠DAB;
(2)探究线段PC,PF之间的大小关系,并加以证明;
(3)若tan∠PCB= ![]() ,BE=
,BE= ![]() ,求PF的长.
,求PF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com