
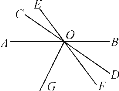
【题目】如图,直线AB,CD,EF相交于点O,OG是∠AOF的平分线,∠BOD=35°,∠COE=18°,则∠COG的度数是________.
【答案】98.5°
【解析】
已知∠BOD、∠COE的度数,根据对顶角相等可求出∠AOC、∠DOF的度数,∠BOD已知,∠DOF已求出,则∠AOF的度数可求出,再根据OG 是∠AOF的平分线,进一步求出∠AOG,再根据∠COG=∠AOC+∠AOG,则∠COG的度数即可求得.
∵∠BOD=35°,
∴∠AOC=35°,
∵∠COE=18°,
∴∠DOF=18°,
∴∠BOF=∠BOD+∠DOF=35°+18°=53°,
∴∠AOF=180°-53°=127°,
∵OG平分∠AOF,
∴∠AOG=∠GOF=![]() ∠AOF=
∠AOF=![]() ×127°=63.5°,
×127°=63.5°,
∴∠COG=∠AOC+∠AOG=35°+63.5°=98.5°.
故答案为:98.5°


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】南水北调中线工程北京段干线工程起自房山北拒马河,经房山区至大宁水库,穿永定河,过丰台,沿西四环路北上至终点颐和园团城湖,全长80公里. 主要采取地下涵管压力输水方式,在输水过程中全程计量、跟踪监测、精细调度、高效配置,确保最大限度利用南水. 北京严格遵循南水北调工程“三先三后”原则,科学制定用水计划,研究确立了“节、喝、存、补”的用水方针,2017-2018年度入京水量达12.10亿立方米,成为历年来北京调水最多的一个调水年度. 如图,在铺设地下管道的时候,需要把拒马河沿线的管道l中的水引到房山水站A,B两处.
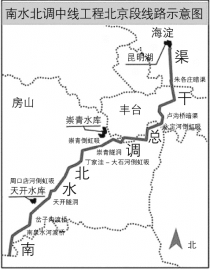

工人师傅设计了一种最节省材料的修建方案如下:


请回答:工人师傅的画图依据是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD, 
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB= ![]() ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( ) 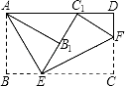
A.![]()
B.2
C.3
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ![]() ,0)
,0)
D.(﹣ ![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子元件厂准备生产1200个电子元件,生产一半后,由于要尽快投入市场,该厂提高了生产效率,每天生产的电子元件个数是原来的1.2倍,结果提前2天完成了任务,求该厂后来每天生产电子元件多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题:①若x=0,则x2﹣2x=0;②若 ![]() =
= ![]() ,则a=b;③矩形既是轴对称图形又是中心对称图形;④圆内接四边形的对角一定相等.其中原命题与逆命题均为真命题的个数是( )
,则a=b;③矩形既是轴对称图形又是中心对称图形;④圆内接四边形的对角一定相等.其中原命题与逆命题均为真命题的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com