
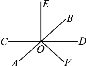
【题目】如图所示,直线AB,CD相交于点O,OE⊥CD于点O,OD平分∠BOF,∠BOE=50°,求∠AOC、∠EOF与∠AOF的度数.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠EBC的度数;
(2)若AD=5,△EBC的周长为16,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南水北调中线工程北京段干线工程起自房山北拒马河,经房山区至大宁水库,穿永定河,过丰台,沿西四环路北上至终点颐和园团城湖,全长80公里. 主要采取地下涵管压力输水方式,在输水过程中全程计量、跟踪监测、精细调度、高效配置,确保最大限度利用南水. 北京严格遵循南水北调工程“三先三后”原则,科学制定用水计划,研究确立了“节、喝、存、补”的用水方针,2017-2018年度入京水量达12.10亿立方米,成为历年来北京调水最多的一个调水年度. 如图,在铺设地下管道的时候,需要把拒马河沿线的管道l中的水引到房山水站A,B两处.
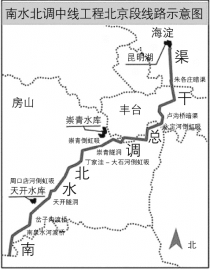

工人师傅设计了一种最节省材料的修建方案如下:


请回答:工人师傅的画图依据是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
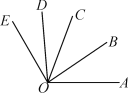
【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOC=70°,∠COE=50°,那么∠BOD是多少度?
(2)如果∠BOD=70°,那么∠AOE是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
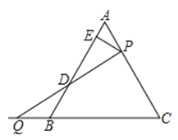
【题目】如图,△ABC 是边长为 6 cm 的等边三角形,P 从点 A 岀发沿 AC 边向 C 运动, 与此同时 Q 从 B 出发以相同的速度沿 CB 延长线方向运动.当 P 到达 C 点时,P、Q 停止运动, 连接 PQ 交 AB 于 D
(1)设 P、Q 的运动速度为 1 cm/s,当运动时间为多少时,∠BQD=30°?
(2)过 P 作 PE⊥AB 于 E,在运动过程中线段 ED 的长是否发生变化?如果不变,求出线段 ED的长;如果变化请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
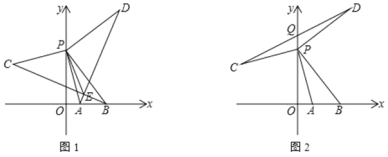
【题目】已知如图,在平面直角坐标系中,点 B(m,0)、A(n,0)分别是 x 轴轴上两点, 且满足多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,点 P(0,h)是 y 轴正半轴上的动点
(1)求三角形△ABP 的面积(用含 h 的代数式表示)
(2)过点 P 作 DP⊥PB,CP⊥PA,且 PD=PB,PC=AP
① 连接 AD、BC 相交于点 E,再连 PE,求∠BEP 的度数
② 连 CD 与 y 轴相交于点 Q,当动点 P 在 y 轴正半轴上运动时,线段 PQ 的长度变不变?如果不变,请求出其值;如果变化,请求出其变化范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD, 
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com