
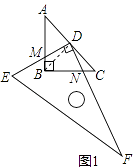
����Ŀ����ͼ1����֪��ABC�У�AB=BC=1����ABC=90�㣬��һ�麬30��ǵ����ǰ�DEF��ֱ�Ƕ���D����AC���е��ϣ�ֱ�����ǰ�Ķ�ֱ�DZ�ΪDE����ֱ�DZ�ΪDF������ֱ�����ǰ�DEF��D�㰴��ʱ�뷽����ת�� 
��1����ͼ1�У�DE��AB��M��DF��BC��N����֤��DM=DN��������һ�����У�ֱ�����ǰ�DEF���ABC���ص�����Ϊ�ı���DMBN����˵���ı���DMBN������Ƿ����仯���������仯����˵������α仯�ģ����������仯������������
��2��������ת����ͼ2��λ�ã��ӳ�AB��DE��M���ӳ�BC��DF��N��DM=DN�Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��3��������ת����ͼ3��λ�ã��ӳ�FD��BC��N���ӳ�ED��AB��M��DM=DN�Ƿ���Ȼ�������������������д�����ۣ�����֤����
���𰸡�
��1���⣺����ͼ1������DB����Rt��ABC�У�AB=BC��AD=DC��
��DB=DC=AD����BDC=90�㣬
���ABD=��C=45�㣬
�ߡ�MDB+��BDN=��CDN+��BDN=90�㣬
���MDB=��NDC��
���BMD�ա�CND��ASA����
��DM=DN��
���ı���DMBN������������仯��
�ɢ�֪��BMD�ա�CND��
��S��BMD=S��CND��
��S�ı���DMBN=S��DBN+S��DMB=S��DBN+S��DNC=S��DBC= ![]() S��ABC=
S��ABC= ![]() ��
�� ![]() =
= ![]() ��
��
��2���⣺DM=DN��Ȼ������
֤������ͼ2������DB����Rt��ABC�У�AB=BC��AD=DC��
��DB=DC����BDC=90�㣬
���DCB=��DBC=45�㣬
���DBM=��DCN=135�㣬
�ߡ�NDC+��CDM=��BDM+��CDM=90�㣬
���CDN=��BDM��
���ڡ�BMD�͡�CND�У�  ��
��
���BMD�ա�CND��ASA����
��DM=DN��

��3���⣺DM=DN��
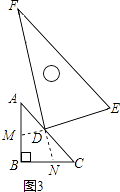
����������1������BD��֤����DMB�ա�DNC��������֪��ȫ�������Ѿ߱���������֤����MDB=��NDC����ASA֤��ȫ�ȣ��ı���DMBN������������仯����Ϊ�������ʼ�յ��ڡ�ABC�����һ�룻��2��������ͬ�����ã�1���е�֤����������֤����DMB�ա�DNC����3��������Ȼ����������ͬ��1����
�����㾫�������յ���ֱ�������κ���ת�������ǽ����ĸ�������Ҫ֪������ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻����ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��ˣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD����࣬�������ȱ�������ADE��DCF������AF��BE.
��1�����жϣ�AF��BE��������ϵ��______________.λ�ù�ϵ��_______________.
��2����ͼ2�����������������ȱ�������ADE��DCF����Ϊ����������������ADE��DCF����EA=ED=FD=FC�����ڣ�1�����еĽ����Ƿ���Ȼ�������������жϲ�����֤��.


��ͼ1�� ��ͼ2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ������PΪ���㻭��P,ʹ��P�����߷ֱ�͡�1�����ߴ�ֱ;
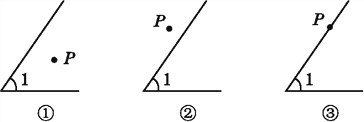
(2)��һ����P�͡�1�Ķ���,����֮���������ϵ������������������;
(3)ͬ����ͼ�ں�ͼ������PΪ��������APB,ʹ��APB�����߷ֱ�͡�1�����ߴ�ֱ,�ֱ�д��ͼ�ں�ͼ���С�APB�͡�1֮���������ϵ(��Ҫ��д������).
ͼ��:��������������������������������,
ͼ��:��������������������������������;
(4)�������������ο��Եõ�һ������:���һ���ǵ����߷ֱ����һ���ǵ����ߴ�ֱ,��ô����������������(��Ҫ��д������).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���ڡ�ABC�У�CA=CB����ACB=90�㣬E��F�ֱ���CA��CB�ߵ����ȷֵ㣬����ECF�Ƶ�C��ʱ����ת���ǣ�0�㣼����90�㣩���õ���MCN������AM��BN�� 
��1����֤��AM=BN��
��2����MA��CNʱ��������ת�Ǧ�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,һ���뾶Ϊ18 cm��Բ,��������ȥһ��������,����ȥ�������εı߳���С���ʱ,ʣ�²��ֵ����Ҳ��֮�����仯.

(1)����ȥ�������α߳�Ϊx(cm),ʣ�²��ֵ����Ϊy(cm2),��y��x֮��Ĺ�ϵʽ��ʲô?
(2)����ȥ�������εı߳���1 cm�仯��9 cmʱ,ʣ�²��ֵ������____�仯��____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF��G�����н��ۣ�
��BE=DF���ڡ�DAF=15�㣬��AC��ֱƽ��EF����BE+DF=EF����S��CEF=2S��ABE ��
������ȷ�����У� ������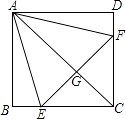
A.4
B.3
C.2
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��DF����D+��B=180����
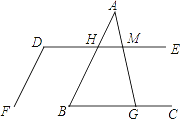
��1����֤��DE��BC��
��2�������AMD=75�������AGC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��2��y1����B��3��y2���Ƕ��κ���y��x2��2x+m��ͼ�������㣬��y1��y2�Ĵ�С��ϵΪy1_____y2���������������������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com