
【题目】Rt△ABC中,∠A=90°,角平分线AE、中线AD、高线AH的大小关系是( )
A.AH<AE<AD
B.AH<AD<AE
C.AH≤AD≤AE
D.AH≤AE≤AD
【答案】D
【解析】①Rt△ABC中,AB=AC;(图①)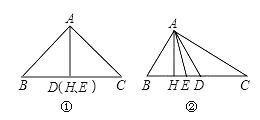
根据等腰三角形三线合一的性质知:
AD、AH、AE互相重合,此时AD=AH=AE;
②Rt△ABC中,AB≠AC;(设AC>AB , 如图②)
在Rt△AHE中,由于AE是斜边,故AE>AH;
同理可证AD>AH;
∵∠AED>∠AHD=90°,∠ADH<∠AHE=90°
∴∠AED>∠ADE;
根据大角对大边知:AD>AE;
即AD>AE>AH;
综上所述,角平分线AE、中线AD、高线AH的大小关系是AH≤AE≤AD;
故选D.
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)).


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2m+1)x+m2﹣4=0有两个不相等的实数根 (Ⅰ)求实数m的取值范围;
(Ⅱ)若两个实数根的平方和等于15,求实数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向点B以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动;如果同时出发,则过3秒时,求△BPQ的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )

A. 4cm B. 6cm C. 8cm D. 10cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= ![]() :3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)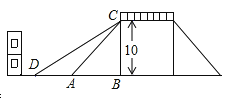
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC= 度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC , ∠B=30°,∠C=60°,E、F、M、N分别为AB、CD、BC、DA的中点,若BC=7,MN=3,则EF为( ) 
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形ABC中,AB=AC,D,E分别为边AB,AC上的点,DM平分∠BDE,EN平分∠DEC,若∠DMN=110°,则∠DEA=( )

A. 40° B. 50° C. 60° D. 70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com