
����Ŀ��Ѵ�ڵ�����ɽ�鱩�����±���¼��ijˮ��![]() ��ˮλ�ı仯���������
��ˮλ�ı仯���������![]() ��ʾʱ��(��λ��
��ʾʱ��(��λ��![]() )��
)��![]() ��ʾˮλ�߶�(��λ��
��ʾˮλ�߶�(��λ��![]() )����
)����![]() ʱ���ﵽ����ˮλ����ʼ��բ��ˮ��
ʱ���ﵽ����ˮλ����ʼ��բ��ˮ��
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 14 | 15 | 16 | 17 | 18 | 14.4 | 12 | 10.3 | 9 | 8 | 7.2 |
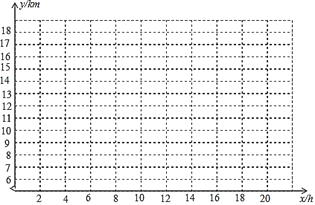
(1)�ڸ�����ƽ��ֱ������ϵ�У����ݱ����е����������Ӧ�ĵ㣮
(2)��ֱ������բ��ˮǰ�ͷ�ˮ������ϱ������ݵĺ�������ʽ��
(3)�ݹ��ƣ���բ��ˮ��ˮλ�����ֱ仯���ɻ������һ��ʱ�䣬Ԥ���ʱˮλ�ﵽ![]() ��
��
���𰸡�(1)��������(2)![]() ��
��![]() ��(3)Ԥ��
��(3)Ԥ��![]() ˮλ�ﵽ
ˮλ�ﵽ![]() ��
��
��������
�����������ƣ��²⺯�����ͣ����ֵ�![]() ʱ��
ʱ��![]() ��
��![]() ������һ�κ�����ϵ����
������һ�κ�����ϵ����![]() ʱ��
ʱ��![]() ��
��![]() �Ͳ���һ�κ�����ϵ��ͨ���۲����ݷ���
�Ͳ���һ�κ�����ϵ��ͨ���۲����ݷ���![]() ��
��![]() �Ĺ�ϵ����Ϸ�����������
�Ĺ�ϵ����Ϸ�����������
(1)��ƽ��ֱ������ϵ�У����ݱ����е����������Ӧ�ĵ㣬��ͼ��ʾ��
(2)�۲�ͼ��![]() ʱ��
ʱ��![]() ��
��![]() ������һ�κ�����ϵ����
������һ�κ�����ϵ����![]() ����
����![]() ��
��![]() �����
�����![]() ����ã�
����ã�![]() ��
��![]() ��
��![]() ��
��![]() �Ĺ�ϵʽΪ��
�Ĺ�ϵʽΪ��![]() ������֤
������֤![]() ��
��![]() ��
��![]() ������
������![]() ����˷�ˮǰ
����˷�ˮǰ![]() ��
��![]() �Ĺ�ϵʽΪ��
�Ĺ�ϵʽΪ��![]() ���۲�ͼ��
���۲�ͼ��![]() ʱ��
ʱ��![]() ��
��![]() �Ͳ���һ�κ�����ϵ��ͨ���۲����ݷ��֣�
�Ͳ���һ�κ�����ϵ��ͨ���۲����ݷ��֣�![]() .��˷�ˮ��
.��˷�ˮ��![]() ��
��![]() �Ĺ�ϵ����Ϸ�������������ϵʽΪ��
�Ĺ�ϵ����Ϸ�������������ϵʽΪ��![]() �����Կ�բ��ˮǰ�ͷ�ˮ������ϱ������ݵĺ�������ʽΪ��
�����Կ�բ��ˮǰ�ͷ�ˮ������ϱ������ݵĺ�������ʽΪ��![]() ��
��![]() .
.
(3)��![]() ʱ��
ʱ��![]() ����ã�
����ã�![]() �����Ԥ��
�����Ԥ��![]() ˮλ�ﵽ
ˮλ�ﵽ![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ��x����A��-2��0����B��1��0������y����C��0��2����
��1������κ����Ľ���ʽ��
��2������AC����ֱ��AC�Ϸ������������Ƿ���ڵ�N��ʹ��NAC�������������ڣ����������ֵ����ʱ��N�����꣬�������ڣ�˵�����ɣ�
��3������M��x���ϣ��Ƿ���ڵ�M��ʹ��B��C��MΪ������������ǵ��������Σ������ڣ�ֱ��д����M�����ꣻ�������ڣ�˵�����ɣ�
��4����PΪ��������һ�㣬��P��PQ��BC��Q����y�������������Ƿ���ڵ�Pʹ��CPQ�ס�BCO����C���B��Ӧ���������ڣ������P�����꣬�������ڣ�˵�����ɣ�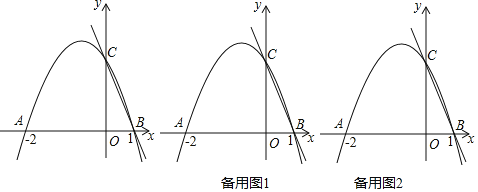
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�AB=3����E��F�ֱ���CD��AD�ϣ�CE=DF��BE��CF�ཻ�ڵ�G����ͼ����Ӱ���ֵ������������ABCD�����֮��Ϊ2��3������BCG���ܳ�Ϊ_____��
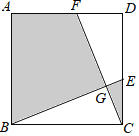
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijƷ��̫������ˮ���IJ���ʾ��ͼ.��֪����ˮƽ���![]() ƽ����ˮƽ��AD,��Ϊ
ƽ����ˮƽ��AD,��Ϊ![]() ����չ�
����չ�![]() ��ˮƽ��
��ˮƽ��![]() �ļн�Ϊ37��,����
�ļн�Ϊ37��,����![]() ����б��
����б��![]() Ϊ22��,������ֱ��
Ϊ22��,������ֱ��![]() �ij���Ϊ05
�ij���Ϊ05 ![]() ������������Ϣ,�������
������������Ϣ,�������

��1��)��չ��϶�![]() ��ˮƽ��
��ˮƽ��![]() �ľ��룻
�ľ��룻
��2)ˮƽ���![]() �ij���(�����ȷ��0.1
�ij���(�����ȷ��0.1 ![]() )���ο����ݣ�
)���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�
�У�![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() ���㣮
���㣮

��1����Բ��![]() �����ꣻ
�����ꣻ
��2����ֱ��![]() ��
��![]() �����ڵ�
�����ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() ����ֱ��
����ֱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��3���ڹ���![]() ����Բ��
����Բ��![]() Ϊ���������������һ����
Ϊ���������������һ����![]() ������
������![]() ��
��![]() �ᣬ��ֱ��
�ᣬ��ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() Ϊ�뾶��
Ϊ�뾶��![]() ��ֱ��
��ֱ��![]() �ཻ����һ��
�ཻ����һ��![]() ����
����![]() ʱ�����
ʱ�����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y��x2��2x+c��cΪ�������ĶԳ�����ͼ��ʾ���������߹���C��0��c����
��1����c����3ʱ���㣨x1��y1����������y��x2��2x+c�ϣ���y1����Сֵ��
��2������������x�����������㣬�������ҷֱ�Ϊ��A��B����OA��![]() OB���������ߵĽ���ʽ��
OB���������ߵĽ���ʽ��
��3������1��x��0ʱ����������x������ֻ��һ�������㣬��c��ȡֵ��Χ��
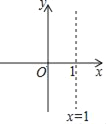
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij�ֶ�ͯ��ߣ����ÿ������Ϊ40Ԫ���г��������Ź涨���������ÿ�������ܳ���60Ԫ����ÿ����۳�50���������г����鷢�֣����۵���ÿ����2Ԫ��ÿ�������������1���������۵�������![]() Ԫ��ÿ���۳�
Ԫ��ÿ���۳�![]() ����
����
��1�����![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��2����![]() Ϊ����ʱ������ÿ������������߿ɻ�����2250Ԫ��
Ϊ����ʱ������ÿ������������߿ɻ�����2250Ԫ��
��3���賬��ÿ������������߿ɻ���![]() Ԫ����
Ԫ����![]() Ϊ����ʱ
Ϊ����ʱ![]() ������ֵ�Ƕ��٣�
������ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣮Ϊ�����л����㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵ���������д��������Ϊ�˽Ȿ�δ����ijɼ���У��ί�����ȡ������200��ѧ���ijɼ���Ϊ��������ͳ�ƣ��Ƴ����²�������ͳ��ͼ����
Ƶ��Ƶ�ʷֲ���
�ɼ�x���֣� | Ƶ�����ˣ� | Ƶ�� |
50��x��60 | 10 | 0.05 |
60��x��70 | 30 | 0.15 |
70��x��80 | 40 | n |
80��x��90 | m | 0.35 |
90��x��100 | 50 | 0.25 |
����������Ϣ������������⣺
��1��m=�� ����n=�� ����
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����200��ѧ���ɼ�����λ���������� �������Σ�
��4�����ɼ���90�����ϣ�����90�֣�Ϊ�������ȣ�������Ƹ�У�μӱ��α�����3000��ѧ���гɼ����������ȵ�Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪������![]() ����
����![]() ��
��
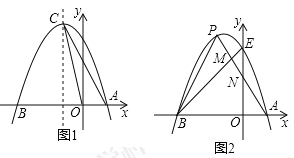
��1���������ߵĽ���ʽ���䶥��C�����ꣻ
��2�����D��x����һ�㣬��![]() ʱ�����D�����ꣻ
ʱ�����D�����ꣻ
��3����ͼ2����������y�ύ�ڵ�E����P�Ǹ���������λ�ڵڶ����ĵ㣬�߶�PA��BE�ڵ�M����y���ڵ�N��![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ����
����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com