
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(-2,0),B(1,0),交y轴于C(0,2);
(1)求二次函数的解析式;
(2)连接AC,在直线AC上方的抛物线上是否存在点N,使△NAC的面积最大,若存在,求出这个最大值及此时点N的坐标,若不存在,说明理由.
(3)若点M在x轴上,是否存在点M,使以B、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由.
(4)若P为抛物线上一点,过P作PQ⊥BC于Q,在y轴左侧的抛物线是否存在点P使△CPQ∽△BCO(点C与点B对应),若存在,求出点P的坐标,若不存在,说明理由.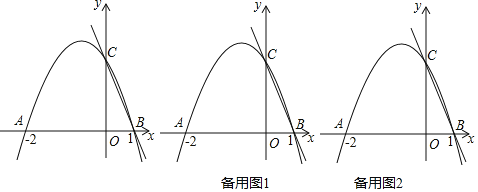
【答案】(1)二次函数的解析式为:y=-x2-x+2;;(2)最大值为1,此时N(-1,2);(3)M的坐标为(-1,0)或(1±![]() ,0)或(-
,0)或(-![]() ,0);(4)点P的坐标为:(-1,2)或(-
,0);(4)点P的坐标为:(-1,2)或(-![]() ,-
,-![]() ).
).
【解析】
(1)利用交点式求二次函数的解析式;
(2)求直线AC的解析式,作辅助线ND,根据抛物线的解析式表示N的坐标,根据直线AC的解析式表示D的坐标,表示ND的长,利用铅直高度与水平宽度的积求三角形ANC的面积,根据二次函数的最值可得面积的最大值,并计算此时N的坐标;
(3)分三种情况:当B、C、M为顶点的三角形是等腰三角形时,分别以三边为腰,画图形,求M的坐标即可;
(4)存在两种情况:①如图4,点P1与点C关于抛物线的对称轴对称时符合条件;
②如图5,图3中的M(-![]() ,0)时,MB=MC,设CM与抛物线交于点P2,则△CP2Q∽△BCO,P2为直线CM的抛物线的交点.
,0)时,MB=MC,设CM与抛物线交于点P2,则△CP2Q∽△BCO,P2为直线CM的抛物线的交点.
(1)∵二次函数y=ax2+bx+c的图象交x轴于A(-2,0),B(1,0),
设二次函数的解析式为:y=a(x+2)(x-1),
把C(0,2)代入得:2=a(0+2)(0-1),
a=-1,
∴y=-(x+2)(x-1)=-x2-x+2,
∴二次函数的解析式为:y=-x2-x+2;
(2)如图1,过N作ND∥y轴,交AC于D,设N(n,-n2-n+2),
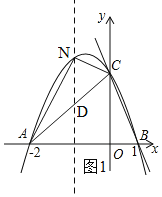
设直线AC的解析式为:y=kx+b,
把A(-2,0)、C(0,2)代入得:![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为:y=x+2,
∴D(n,n+2),
∴ND=(-n2-n+2)-(n+2)=-n2-2n,
∴S△ANC=![]() ×2×[-n2-2n]=-n2-2n=-(n+1)2+1,
×2×[-n2-2n]=-n2-2n=-(n+1)2+1,
∴当n=-1时,△ANC的面积有最大值为1,此时N(-1,2),
(3)存在,分三种情况:
①如图2,当BC=CM1时,M1(-1,0);
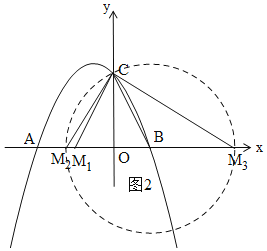
②如图2,由勾股定理得:BC=![]() ,
,
以B为圆心,以BC为半径画圆,交x轴于M2、M3,则BC=BM2=BM3=![]() ,
,
此时,M2(1-![]() ,0),M3(1+
,0),M3(1+![]() ,0);
,0);
③如图3,作BC的中垂线,交x轴于M4,连接CM4,则CM4=BM4,
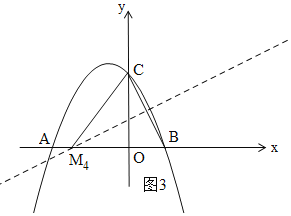
设OM4=x,则CM4=BM4=x+1,
由勾股定理得:22+x2=(1+x)2,
解得:x=![]() ,
,
∵M4在x轴的负半轴上,
∴M4(-![]() ,0),
,0),
综上所述,当B、C、M为顶点的三角形是等腰三角形时,M的坐标为(-1,0)或(1±![]() ,0)或(-
,0)或(-![]() ,0);
,0);
(4)存在两种情况:
①如图4,过C作x轴的平行线交抛物线于P1,过P1作P1Q⊥BC,
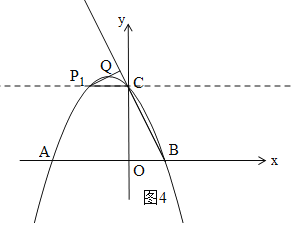
此时,△CP1Q∽△BCO,
∴点P1与点C关于抛物线的对称轴对称,
∴P1(-1,2),
②如图5,由(3)知:当M(-![]() ,0)时,MB=MC,设CM与抛物线交于点P2,
,0)时,MB=MC,设CM与抛物线交于点P2,
过P2作P2Q⊥BC,此时,△CP2Q∽△BCO,
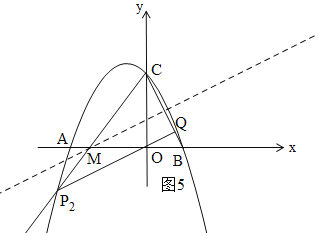
易得直线CM的解析式为:y=![]() x+2,
x+2,
则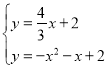 ,
,
解得:P2(-![]() ,-
,-![]() ),
),
综上所述,点P的坐标为:(-1,2)或(-![]() ,-
,-![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:小明为了计算![]() 的值 ,采用以下方法:
的值 ,采用以下方法:
设![]() ①
①
则![]() ②
②
②-①得 ![]()
∴![]()
(1)![]() = ;
= ;
(2)![]() = ;
= ;
(3)求![]() 的和(
的和(![]() ,
,![]() 是正整数,请写出计算过程 ).
是正整数,请写出计算过程 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂长
的等腰直角三角形,摆动臂长![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
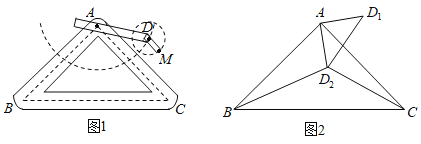
(1)在旋转过程中:
①当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的长;
的长;
②当![]() 三点在同一直角三角形的顶点时,求
三点在同一直角三角形的顶点时,求![]() 的长.
的长.
(2)若摆动臂![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=﹣x2+bx+3与x轴的一个交点为(1,0),顶点记为A,抛物线C2与抛物线C1关于y轴对称.
(1)求抛物线C2的函数表达式;
(2)若抛物线C2与x轴正半轴的交点记作B,在x轴上是否存在一点P,使△PAB为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
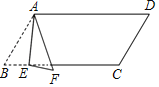
【题目】如图,在ABCD中,∠B=60°,AB=6,BC=12.点E是BC上一动点,将△ABE沿直线AE折叠,得到△AFE,则当AF与ABCD的边垂直时,BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汛期到来,山洪暴发.下表记录了某水库![]() 内水位的变化情况,其中
内水位的变化情况,其中![]() 表示时间(单位:
表示时间(单位:![]() ),
),![]() 表示水位高度(单位:
表示水位高度(单位:![]() ),当
),当![]() 时,达到警戒水位,开始开闸放水.
时,达到警戒水位,开始开闸放水.
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 14 | 15 | 16 | 17 | 18 | 14.4 | 12 | 10.3 | 9 | 8 | 7.2 |
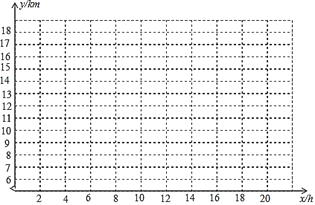
(1)在给出的平面直角坐标系中,根据表格中的数据描出相应的点.
(2)请分别求出开闸放水前和放水后最符合表中数据的函数解析式.
(3)据估计,开闸放水后,水位的这种变化规律还会持续一段时间,预测何时水位达到![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com