
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂长
的等腰直角三角形,摆动臂长![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
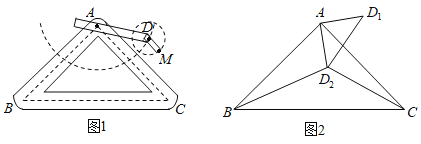
(1)在旋转过程中:
①当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的长;
的长;
②当![]() 三点在同一直角三角形的顶点时,求
三点在同一直角三角形的顶点时,求![]() 的长.
的长.
(2)若摆动臂![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
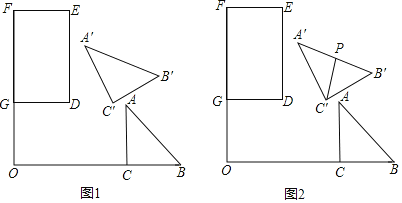
【题目】如图1,矩形DEFG中,DG=2,DE=3,Rt△ABC中,∠ACB=90°,CA=CB=2,FG,BC的延长线相交于点O,且FG⊥BC,OG=2,OC=4.将△ABC绕点O逆时针旋转α(0°≤α<180°)得到△A′B′C′.
(1)当α=30°时,求点C′到直线OF的距离.
(2)在图1中,取A′B′的中点P,连结C′P,如图2.
①当C′P与矩形DEFG的一条边平行时,求点C′到直线DE的距离.
②当线段A′P与矩形DEFG的边有且只有一个交点时,求该交点到直线DG的距离的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)的图象与x轴交于A,B两点,与y轴正半轴交于点C,它的对称轴为直线x=﹣1.则下列选项中正确的是( )
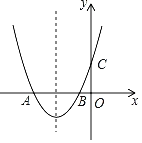
A.abc<0B.4ac﹣b2>0
C.c﹣a>0D.当x=﹣n2﹣2(n为实数)时,y≥c
查看答案和解析>>
科目:初中数学 来源: 题型:
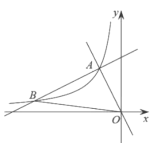
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区游泳馆夏季推出两种收费方式.方式一:先购买会员证,会员证200元,只限本人当年使用,凭证游泳每次需另付费10元:方式二:不购买会员证,每次游泳需付费20元.
(1)若甲计划今年夏季游泳的费用为500元,则选择哪种付费方式游泳次数比较多?
(2)若乙计划今年夏季游泳的次数超过15次,则选择哪种付费方式游泳花费比较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,连接
的中点,连接![]() ,
,![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 对折,得到
对折,得到![]() ,延长
,延长![]() 交
交![]() 延长线于点
延长线于点![]() ,下列4个结论:①
,下列4个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;正确的结论有__________
;正确的结论有__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点(不与A、B重合),D为的![]() 中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.
中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.
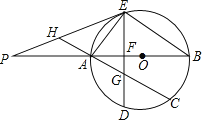
(1)求证:PE是⊙O的切线;
(2)连接CA与DE相交于点G,CA的延长线交PE于H,求证:HE=HG;
(3)若tan∠P=![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com