
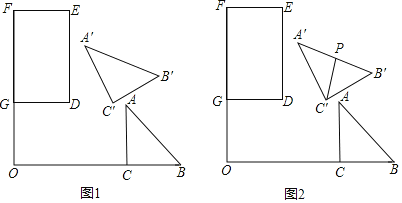
ЁОЬтФПЁПШчЭМ1ЃЌОиаЮDEFGжаЃЌDGЃН2ЃЌDEЃН3ЃЌRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌCAЃНCBЃН2ЃЌFGЃЌBCЕФбгГЄЯпЯрНЛгкЕуOЃЌЧвFGЁЭBCЃЌOGЃН2ЃЌOCЃН4ЃЎНЋЁїABCШЦЕуOФцЪБеыа§зЊІСЃЈ0ЁуЁмІСЃМ180ЁуЃЉЕУЕНЁїAЁфBЁфCЁфЃЎ
ЃЈ1ЃЉЕБІСЃН30ЁуЪБЃЌЧѓЕуCЁфЕНжБЯпOFЕФОрРыЃЎ
ЃЈ2ЃЉдкЭМ1жаЃЌШЁAЁфBЁфЕФжаЕуPЃЌСЌНсCЁфPЃЌШчЭМ2ЃЎ
ЂйЕБCЁфPгыОиаЮDEFGЕФвЛЬѕБпЦНааЪБЃЌЧѓЕуCЁфЕНжБЯпDEЕФОрРыЃЎ
ЂкЕБЯпЖЮAЁфPгыОиаЮDEFGЕФБпгаЧвжЛгавЛИіНЛЕуЪБЃЌЧѓИУНЛЕуЕНжБЯпDGЕФОрРыЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЕуCЁфЕНжБЯпOFЕФОрРыЮЊ2![]() ЃЛЃЈ2ЃЉЂйЕуCЁфЕНжБЯпDEЕФОрРыЮЊ2
ЃЛЃЈ2ЃЉЂйЕуCЁфЕНжБЯпDEЕФОрРыЮЊ2![]() +2ЃЛЂк2ЁмdЁм
+2ЃЛЂк2ЁмdЁм![]() Љ2ЛђdЃН3ЃЎ
Љ2ЛђdЃН3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§ЕуCЁфзїCЁфHЁЭOFгкHЃЎИљОнжБНЧШ§НЧаЮЕФБпНЧЙиЯЕЃЌНтжБНЧШ§НЧаЮЧѓГіCHМДПЩЃЎ
ЃЈ2ЃЉЂйЗжСНжжЧщаЮЃКЕБCЁфPЁЮOFЪБЃЌЙ§ЕуCЁфзїCЁфMЁЭOFгкMЃЛЕБCЁфPЁЮDGЪБЃЌЙ§ЕуCЁфзїCЁфNЁЭFGгкNЃЎЭЈЙ§НтжБНЧШ§НЧаЮЃЌЗжБ№ЧѓГіCЁфMЃЌCЁфNМДПЩЃЎ
ЂкЩшdЮЊЫљЧѓЕФОрРыЃЎЕквЛжжЧщаЮЃКЕБЕуAЁфТфдкDEЩЯЪБЃЌСЌНгOAЁфЃЌбгГЄEDНЛOCгкMЃЎЕБЕуPТфдкDEЩЯЪБЃЌСЌНгOPЃЌЙ§ЕуPзїPQЁЭCЁфBЁфгкQЃЎНсКЯЭМЯѓПЩЕУНсТлЃЎ
ЕкЖўжжЧщаЮЃКЕБAЁфPгыFGЯрНЛЃЌВЛгыEFЯрНЛЪБЃЌЕБЕуAЁфдкFGЩЯЪБЃЌAЁфGЃН2![]() Љ2ЃЌМДdЃН2
Љ2ЃЌМДdЃН2![]() Љ2ЃЛЕБЕуPТфдкEFЩЯЪБЃЌЩшOFНЛAЁфBЁфгкQЃЌЙ§ЕуPзїPTЁЭBЁфCЁфгкTЃЌЙ§ЕуPзїPRЁЮOQНЛOBЁфгкRЃЌСЌНгOPЃЎЧѓГіQGПЩЕУНсТлЃЎ
Љ2ЃЛЕБЕуPТфдкEFЩЯЪБЃЌЩшOFНЛAЁфBЁфгкQЃЌЙ§ЕуPзїPTЁЭBЁфCЁфгкTЃЌЙ§ЕуPзїPRЁЮOQНЛOBЁфгкRЃЌСЌНгOPЃЎЧѓГіQGПЩЕУНсТлЃЎ
ЕкШ§жжЧщаЮЃКЕБAЁфPОЙ§ЕуFЪБЃЌДЫЪБЯдШЛdЃН3ЃЎзлЩЯЫљЪіМДПЩЕУНсТлЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌ
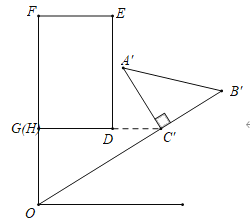
Й§ЕуCЁфзїCЁфHЁЭOFгкHЃЎ
ЁпЁїAЁфBЁфCЁфЪЧгЩЁїABCШЦЕуOФцЪБеыа§зЊЕУЕНЃЌ
ЁрCЁфO=CO=4ЃЌ
дкRtЁїHCЁфжаЃЌ
ЁпЁЯHCЁфOЃНІСЃН30ЁуЃЌ
ЁрCЁфHЃНCЁфOcos30ЁуЃН2![]() ЃЌ
ЃЌ
ЁрЕуCЁфЕНжБЯпOFЕФОрРыЮЊ2![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂйШчЭМЃЌЕБCЁфPЁЮOFЪБЃЌЙ§ЕуCЁфзїCЁфMЁЭOFгкMЃЎ
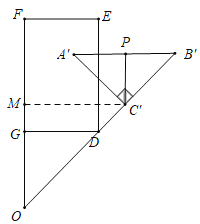
ЁпЁїAЁфBЁфCЁфЮЊЕШбќжБНЧШ§НЧаЮЃЌPЮЊAЁфBЁфЕФжаЕуЃЌ
ЁрЁЯAЁфCЁфP=45ЁуЃЌ
ЁпЁЯAЁфBЁфO=90ЁуЃЌ
ЁрЁЯOCЁфP=135Ёу.
ЁпCЁфPЁЮOFЃЌ
ЁрЁЯOЃН180ЁуЉЁЯOCЁфPЃН45ЁуЃЌ
ЁрЁїOCЁфMЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁпOCЁфЃН4ЃЌ
ЁрCЁфMЃНCЁфOcos45Ёу=4ЁС![]() =
=![]() ЃЌ
ЃЌ
ЁрЕуCЁфЕНжБЯпDEЕФОрРыЮЊ![]() ЃЎ
ЃЎ
ШчЭМЃЌЕБCЁфPЁЮDGЪБЃЌЙ§ЕуCЁфзїCЁфNЁЭFGгкNЃЎ
ЭЌЗЈПЩжЄЁїOCЁфNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрCЁфNЃН![]() ЃЌ
ЃЌ
ЁпGD=2ЃЌ
ЁрЕуCЁфЕНжБЯпDEЕФОрРыЮЊ![]() ЃЎ
ЃЎ
ЂкЩшdЮЊЫљЧѓЕФОрРыЃЎ
ЕквЛжжЧщаЮЃКШчЭМЃЌЕБЕуAЁфТфдкDEЩЯЪБЃЌСЌНгOAЁфЃЌбгГЄEDНЛOCгкMЃЎ
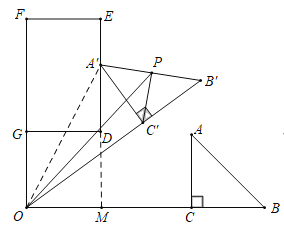
ЁпOC=4ЃЌAC=2ЃЌЁЯACO=90ЁуЃЌ
![]()
ЁпOMЃН2ЃЌЁЯOMAЁфЃН90ЁуЃЌ
ЁрAЁфMЃН![]() ЃН
ЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
гжЁпOG=2ЃЌ
ЁрDM=2ЃЌ
ЁрAЁфDЃНAЁфM-DM=4-2=2ЃЌ
МДdЃН2ЃЌ
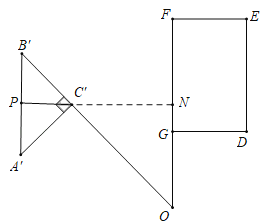
ШчЭМЃЌЕБЕуPТфдкDEЩЯЪБЃЌСЌНгOPЃЌЙ§ЕуPзїPQЁЭCЁфBЁфгкQЃЎ
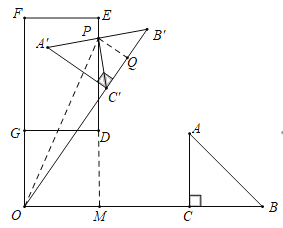
ЁпPЮЊAЁфBЁфЕФжаЕуЃЌЁЯAЁфCЁфBЁф=90ЁуЃЌ
ЁрPQЁЮAЁфCЁфЃЌ
Ёр![]()
ЁпBЁфCЁф=2
ЁрPQЃН1ЃЌCQ=1ЃЌ
ЁрQЕуЮЊBЁфCЁфЕФжаЕуЃЌвВЪЧа§зЊЧАBCЕФжаЕуЃЌ
ЁрOQ=OC+CQ=5
ЁрOPЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрPMЃН![]() ЃЌ
ЃЌ
ЁрPDЃН![]() ЃЌ
ЃЌ
ЁрdЃН![]() Љ2ЃЌ
Љ2ЃЌ
Ёр2ЁмdЁм![]() Љ2ЃЎ
Љ2ЃЎ
ЕкЖўжжЧщаЮЃКЕБAЁфPгыFGЯрНЛЃЌВЛгыEFЯрНЛЪБЃЌЕБЕуAЁфдкFGЩЯЪБЃЌAЁфGЃН2![]() Љ2ЃЌМДdЃН2
Љ2ЃЌМДdЃН2![]() Љ2ЃЌ
Љ2ЃЌ
ШчЭМЃЌЕБЕуPТфдкEFЩЯЪБЃЌЩшOFНЛAЁфBЁфгкQЃЌЙ§ЕуPзїPTЁЭBЁфCЁфгкTЃЌЙ§ЕуPзїPRЁЮOQНЛOBЁфгкRЃЌСЌНгOPЃЎ
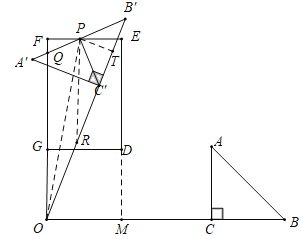
гЩЩЯПЩжЊOPЃН![]() ЃЌOFЃН5ЃЌ
ЃЌOFЃН5ЃЌ
ЁрFPЃН![]() ЃН
ЃН![]() ЃН1ЃЌ
ЃН1ЃЌ
ЁпOFЃНOTЃЌPFЃНPTЃЌЁЯFЃНЁЯPTOЃН90ЁуЃЌ
ЁрRtЁїOPFЁеRtЁїOPTЃЈHLЃЉЃЌ
ЁрЁЯFOPЃНЁЯTOPЃЌ
ЁпPQЁЮOQЃЌ
ЁрЁЯOPRЃНЁЯPOFЃЌ
ЁрЁЯOPRЃНЁЯPORЃЌ
ЁрORЃНPRЃЌ
ЁпPT2+TR2ЃНPR2ЃЌ
![]()
ЁрPRЃН2.6ЃЌRTЃН2.4ЃЌ
ЁпЁїBЁфPRЁзЁїBЁфQOЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрOQЃН![]() ЃЌ
ЃЌ
ЁрQGЃНOQЉOGЃН![]() ЃЌМДdЃН
ЃЌМДdЃН![]()
Ёр2![]() Љ2ЁмdЃМ
Љ2ЁмdЃМ![]() ЃЌ
ЃЌ
ЕкШ§жжЧщаЮЃКЕБAЁфPОЙ§ЕуFЪБЃЌШчЭМЃЌ
ДЫЪБFG=3ЃЌМДdЃН3ЃЎ
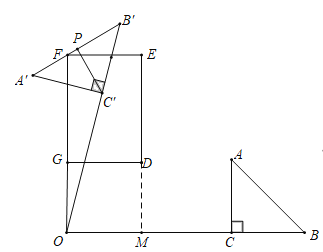
злЩЯЫљЪіЃЌ2ЁмdЁм![]() Љ2ЛђdЃН3ЃЎ
Љ2ЛђdЃН3ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЉгы
ЃЉгы![]() жсНЛгкAЁЂBСНЕуЃЈЕуBдкAЕФгвВрЃЉЃЌгы
жсНЛгкAЁЂBСНЕуЃЈЕуBдкAЕФгвВрЃЉЃЌгы![]() жсНЛгкЕуCЃЌDЪЧХзЮяЯпЕФЖЅЕу.
жсНЛгкЕуCЃЌDЪЧХзЮяЯпЕФЖЅЕу.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓЖЅЕуD ЕФзјБъ
ЪБЃЌЧѓЖЅЕуD ЕФзјБъ
ЃЈ2ЃЉШєOD = OBЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЩшEЮЊAЃЌBСНЕуМфХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЈКЌЖЫЕуAЃЌBЃЉЃЌЙ§ЕуEзїEHЁЭ![]() жсЃЌДЙзуЮЊHЃЌНЛжБЯпBCгкЕуF. МЧЯпЖЮEFЕФГЄЮЊtЃЌШєtЕФзюДѓжЕЮЊ
жсЃЌДЙзуЮЊHЃЌНЛжБЯпBCгкЕуF. МЧЯпЖЮEFЕФГЄЮЊtЃЌШєtЕФзюДѓжЕЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛзщЪ§Он3ЃЌ4ЃЌ4ЃЌ5ЃЌШєЬэМгвЛИіЪ§4ЃЌдђЗЂЩњБфЛЏЕФЭГМЦСПЪЧ( )
A.ЦНОљЪ§B.жкЪ§C.жаЮЛЪ§D.ЗНВю
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕу![]() ЁЂ
ЁЂ![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() гк
гк![]() ЕуЃЌЧв
ЕуЃЌЧв![]() ЃЌвд
ЃЌвд![]() ЮЊжБОЖдк
ЮЊжБОЖдк![]() ЕФзѓВрзїАыдВ
ЕФзѓВрзїАыдВ![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌЧв
ЃЌЧв![]() .
.
ЃЈ1ЃЉШєАыдВ![]() ЩЯгавЛЕу
ЩЯгавЛЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФзюДѓжЕЮЊ________ЃЛ
ЕФзюДѓжЕЮЊ________ЃЛ
ЃЈ2ЃЉЯђгвбижБЯп![]() ЦНвЦ
ЦНвЦ![]() ЕУЕН
ЕУЕН![]() ЃЛ
ЃЛ
ЂйШчЭМЃЌШє![]() НиАыдВ
НиАыдВ![]() ЕФ
ЕФ![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЂкЕБАыдВ![]() гы
гы![]() ЕФБпЯрЧаЪБЃЌЧѓЦНвЦОрРы.
ЕФБпЯрЧаЪБЃЌЧѓЦНвЦОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
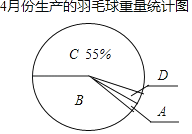
ЁОЬтФПЁПвЛжЛг№УЋЧђЕФжиСПКЯИёБъзМЪЧ5.0ПЫЁЋ5.2ПЫЃЈКЌ5.0ПЫЃЌВЛКЌ5.2ПЫЃЉЃЌФГГЇЖд4дТЗнЩњВњЕФг№УЋЧђжиСПНјааГщбљМьбщЃЎВЂНЋЫљЕУЪ§ОнЛцжЦГЩШчЭМЭГМЦЭМБэЃЎ
4дТЗнЩњВњЕФг№УЋЧђжиСПЭГМЦБэ
зщБ№ | жиСПxЃЈПЫЃЉ | Ъ§СПЃЈжЛЃЉ |
A | xЃМ5.0 | m |
B | 5.0ЁмxЃМ5.1 | 400 |
C | 5.1ЁмxЃМ5.2 | 550 |
D | xЁн5.2 | 30 |
ЃЈ1ЃЉЧѓБэжаmЕФжЕМАЭМжаBзщЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЎ
ЃЈ2ЃЉЮЪетаЉГщбљМьбщЕФг№УЋЧђжаЃЌКЯИёТЪЪЧЖрЩйЃПШчЙћЙКЕУ4дТЗнЩњВњЕФг№УЋЧђ10ЭВЃЈУПЭВ12жЛЃЉЃЌЙРМЦЫљЙКЕУЕФг№УЋЧђжаЃЌЗЧКЯИёЦЗЕФг№УЋЧђгаЖрЩйжЛЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
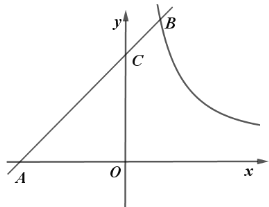
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгк
ЕФЭМЯѓНЛгк![]() ЃЌгы
ЃЌгы![]() жсНЛгк
жсНЛгк![]() ЃЌгы
ЃЌгы![]() жсНЛгк
жсНЛгк![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБНгаДГіВЛЕШЪНЃК![]() ЕФНтМЏЃЛ
ЕФНтМЏЃЛ
ЃЈ3ЃЉ![]() ЪЧ
ЪЧ![]() жсЩЯвЛЖЏЕуЃЌжБНгаДГі
жсЩЯвЛЖЏЕуЃЌжБНгаДГі![]() НаЕФзюДѓжЕКЭДЫЪБЕу
НаЕФзюДѓжЕКЭДЫЪБЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
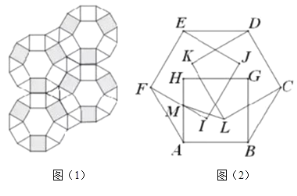
ЁОЬтФПЁПНЈжўЙЄШЫгУБпГЄЯрЕШЕФе§СљБпаЮЁЂе§ЗНаЮЁЂе§Ш§НЧаЮШ§жжДЩзЉЦЬЩшЕиУцЃЌе§ЗНаЮДЩзЉЗжКкАзСНжжбеЩЋЃЌУмЦЬГЩЭМЃЈ1ЃЉЕФаЮзДЃЎгУЫЎФрННжўЧАЃЌЮЊЗНБуЪЉЙЄЃЌЙЄШЫвЊЯШАбДЩзЉАДЭМ1ЗНЪНЯШАкЗХКУЃЌвЛЙЄШЫАкЗХЪБЃЌЮовтМфНЋ3ПщКкЩЋе§ЗНаЮДЩзЉЩЯЗЕНвЛИіе§СљБпаЮЕФЩЯУцЃЌЦфжаШ§Иіе§ЗНаЮЕФвЛЬѕБпЗжБ№КЭе§СљБпаЮЕФШ§ЬѕБпжиКЯЃЌШчЭМЃЈ2ЃЉЫљЪОЃЎАДЭМЃЈ2ЃЉЗНЪНИјИїЕузїЩЯБъзЂЃЌШєе§ЗНаЮЕФБпГЄ![]() ЃЌдђ
ЃЌдђ![]() _____
_____![]() (ВЛПМТЧДЩзЉЕФКёЖШ)
(ВЛПМТЧДЩзЉЕФКёЖШ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіВЛЭИУїЕФДќзгРязАга4ИіаЁЧђЃЌЗжБ№Бъга1ЃЌ2ЃЌ3ЃЌ7ЫФИіЪ§зжЃЌетаЉаЁЧђГ§ЫљБъЪ§зжВЛЭЌЭтЃЌЦфгрЗНУцЭъШЋЯрЭЌЃЌМзЁЂввСНШЫУПДЮЭЌЪБДгДќзгжаИїЫцЛњУўГівЛИіаЁЧђЃЌМЧЯТаЁЧђЩЯЕФЪ§зжЃЌВЂМЦЫуЫќУЧЕФКЭ.
ЃЈ1ЃЉЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓСНЪ§КЭЪЧ8ЕФИХТЪЃЛ
ЃЈ2ЃЉМзЁЂввСНШЫЯыгУетжжЗНЗЈзігЮЯЗЃЌЫћУЧЙцЖЈЃКШєСНЪ§жЎКЭЪЧ2ЕФБЖЪ§ЪБЃЌМзЕУ3ЗжЃЛШєСНЪ§жЎКЭЪЧ3ЕФБЖЪ§ЪБЃЌввЕУ2ЗжЃЛЕБСНЪ§жЎКЭЪЧЦфЫћЪ§жЕЪБЃЌСНШЫОљВЛЕУЗж.ФуШЯЮЊетИігЮЯЗЙЋЦНТ№ЃПЧыЫЕУїРэгЩЃЛШєФуШЯЮЊВЛЙЋЦНЃЌЧыФуаоИФЕУЗжЙцдђЃЌЪЙгЮЯЗЙЋЦНЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
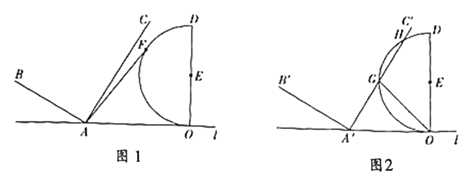
ЁОЬтФПЁПШчЭМ1ЪЧЪЕбщЪвжаЕФвЛжжАкЖЏзАжУЃЌ![]() дкЕиУцЩЯЃЌжЇМм
дкЕиУцЩЯЃЌжЇМм![]() ЪЧЕзБпЮЊ
ЪЧЕзБпЮЊ![]() ЕФЕШбќжБНЧШ§НЧаЮЃЌАкЖЏБлГЄ
ЕФЕШбќжБНЧШ§НЧаЮЃЌАкЖЏБлГЄ![]() ПЩШЦЕу
ПЩШЦЕу![]() а§зЊЃЌАкЖЏБл
а§зЊЃЌАкЖЏБл![]() ПЩШЦЕу
ПЩШЦЕу![]() а§зЊЃЌ
а§зЊЃЌ![]() ЃЌ
ЃЌ![]() .
.
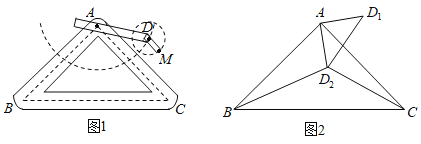
ЃЈ1ЃЉдка§зЊЙ§ГЬжаЃК
ЂйЕБ![]() Ш§ЕудкЭЌвЛжБЯпЩЯЪБЃЌЧѓ
Ш§ЕудкЭЌвЛжБЯпЩЯЪБЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЂкЕБ![]() Ш§ЕудкЭЌвЛжБНЧШ§НЧаЮЕФЖЅЕуЪБЃЌЧѓ
Ш§ЕудкЭЌвЛжБНЧШ§НЧаЮЕФЖЅЕуЪБЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ЃЈ2ЃЉШєАкЖЏБл![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФЮЛжУгЩ
ЕФЮЛжУгЩ![]() ЭтЕФЕу
ЭтЕФЕу![]() зЊЕНЦфФкЕФЕу
зЊЕНЦфФкЕФЕу![]() ДІЃЌСЌНс
ДІЃЌСЌНс![]() ЃЌШчЭМ2ЃЌДЫЪБ
ЃЌШчЭМ2ЃЌДЫЪБ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com