
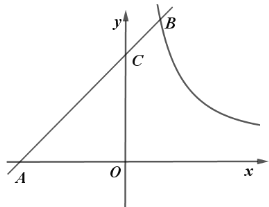
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,与
,与![]() 轴交于
轴交于![]() ,与
,与![]() 轴交于
轴交于![]() ,且
,且![]() .
.
(1)求一次函数与反比例函数的解析式;
(2)直接写出不等式:![]() 的解集;
的解集;
(3)![]() 是
是![]() 轴上一动点,直接写出
轴上一动点,直接写出![]() 叫的最大值和此时点
叫的最大值和此时点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的最大值为
的最大值为![]() ,此时P点坐标为
,此时P点坐标为![]()
【解析】
(1)过![]() 作
作![]() 轴于
轴于![]() ,得
,得![]() ,
,![]() ,可求得
,可求得![]() ,即得到A点坐标,将A点坐标代入
,即得到A点坐标,将A点坐标代入![]() ,可求得b,把
,可求得b,把![]() 代入
代入![]() ,可求得m,进而求得反比例函数解析式;
,可求得m,进而求得反比例函数解析式;
(2)求![]() 的解集,即为求反比例函数大于一次函数时自变量的范围,由图可知当
的解集,即为求反比例函数大于一次函数时自变量的范围,由图可知当![]() 时,
时,![]()
(3)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,
,![]() 的延长线于
的延长线于![]() 轴的交点即为所求点
轴的交点即为所求点![]() ,求得直线
,求得直线![]() 的解析式,即可求出P点坐标及
的解析式,即可求出P点坐标及![]() 值,此时
值,此时![]() 值最大,即为
值最大,即为![]() .
.
(1)过![]() 作
作![]() 轴于
轴于![]() ,
,
∴![]() 轴,
轴,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]()
把![]() 代入
代入![]() 得:
得:![]()
把![]() 代入
代入![]() 得:
得:![]() ,
,
∴![]()
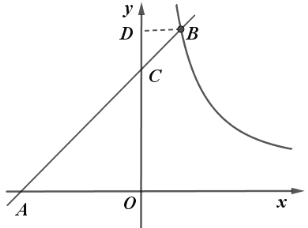
故答案为:![]() ,
,![]()
(2)由图象可知当![]() 时,
时,![]()
故答案为:![]()
(3)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,
,![]() 的延长线于
的延长线于![]() 轴的交点即为所求点
轴的交点即为所求点![]()
∵![]()
∴![]()
∵![]()
设直线![]() 的解析式为y=kx+b
的解析式为y=kx+b
∴![]()
解得![]()
∴直线![]() 的解析式为y=2x+6
的解析式为y=2x+6
当x=0时,y=6
∴![]()
![]() 的最大值为
的最大值为![]()
![]()
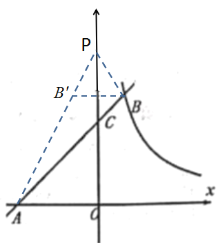
故答案为:![]() 的最大值为
的最大值为![]() ,此时P点坐标为
,此时P点坐标为![]()


科目:初中数学 来源: 题型:
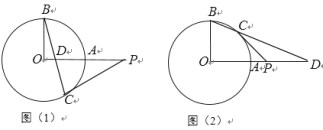
【题目】在⊙O中,半径OA丄OB,点D在OA或OA的延长线上(不与点O,A重合),直线BD交⊙O于点C,过C作⊙O的切线交直线OA于点P.
(1)如图(1),点D在线段OA上,若∠OBC=15°, 求∠OPC的大小;
(2)如图(2),点D在OA的延长线上,若∠OBC=65°,求∠OPC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两条邻边长分别为![]() ,1的矩形纸片剪成四个等腰三角形纸片(无余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的_____(填序号).
,1的矩形纸片剪成四个等腰三角形纸片(无余纸片),各种剪法剪出的等腰三角形中,其中一个等腰三角形的腰长可以是下列数中的_____(填序号).
①![]() ,②1,③
,②1,③![]() ﹣1,④
﹣1,④![]() ,⑤
,⑤![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形DEFG中,DG=2,DE=3,Rt△ABC中,∠ACB=90°,CA=CB=2,FG,BC的延长线相交于点O,且FG⊥BC,OG=2,OC=4.将△ABC绕点O逆时针旋转α(0°≤α<180°)得到△A′B′C′.
(1)当α=30°时,求点C′到直线OF的距离.
(2)在图1中,取A′B′的中点P,连结C′P,如图2.
①当C′P与矩形DEFG的一条边平行时,求点C′到直线DE的距离.
②当线段A′P与矩形DEFG的边有且只有一个交点时,求该交点到直线DG的距离的取值范围.
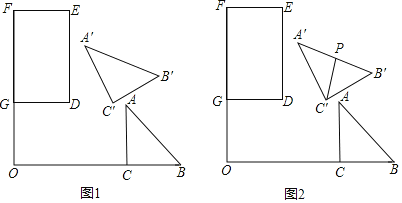
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发行了两枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理,如图的勾股图中,已知![]() ,
,![]() ,
,![]() .作四边形
.作四边形![]() ,满足点
,满足点![]() 、
、![]() 在边
在边![]() 上,点
上,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,
,![]() 、
、![]() 是直线
是直线![]() 与
与![]() ,
,![]() 的交点.那么
的交点.那么![]() 的长等于( )
的长等于( )

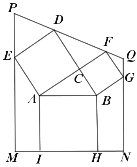
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以π cm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为______时,BP与⊙O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q;
(i)当点P与A,B两点不重合时,求![]() 的值;
的值;
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
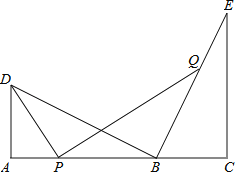
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区游泳馆夏季推出两种收费方式.方式一:先购买会员证,会员证200元,只限本人当年使用,凭证游泳每次需另付费10元:方式二:不购买会员证,每次游泳需付费20元.
(1)若甲计划今年夏季游泳的费用为500元,则选择哪种付费方式游泳次数比较多?
(2)若乙计划今年夏季游泳的次数超过15次,则选择哪种付费方式游泳花费比较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com