
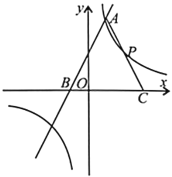
【题目】如图,已知AB是⊙O的直径,C是⊙O上一点(不与A、B重合),D为的![]() 中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.
中点,过点D作弦DE⊥AB于F,P是BA延长线上一点,且∠PEA=∠B.
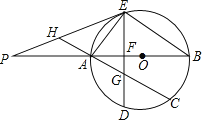
(1)求证:PE是⊙O的切线;
(2)连接CA与DE相交于点G,CA的延长线交PE于H,求证:HE=HG;
(3)若tan∠P=![]() ,试求
,试求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接OE,由圆周角定理证得∠EAB+∠B=90°,可得出∠OAE=∠AEO,则∠PEA+∠AEO=90°,即∠PEO=90°,则结论得证;
(2)连接OD,证得∠AOD=∠AGF,∠B=∠AEF,可得出∠PEF=2∠B,∠AOD=2∠B,可证得∠PEF=∠AOD=∠AGF,则结论得证;
(3)可得出tan∠P=tan∠ODF=![]() ,设OF=5x,则DF=12x,求出AE,BE,得出
,设OF=5x,则DF=12x,求出AE,BE,得出![]() ,证明△PEA∽△PBE,得出
,证明△PEA∽△PBE,得出![]() ,过点H作HK⊥PA于点K,证明∠P=∠PAH,得出PH=AH,设HK=5a,PK=12a,得出PH=13a,可得出AH=13a,AG=10a,则可得出答案.
,过点H作HK⊥PA于点K,证明∠P=∠PAH,得出PH=AH,设HK=5a,PK=12a,得出PH=13a,可得出AH=13a,AG=10a,则可得出答案.
解:(1)证明:如图1,连接OE,
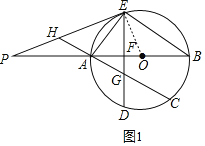
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠EAB+∠B=90°,
∵OA=OE,
∴∠OAE=∠AEO,
∴∠B+∠AEO=90°,
∵∠PEA=∠B,
∴∠PEA+∠AEO=90°,
∴∠PEO=90°,
又∵OE为半径,
∴PE是⊙O的切线;
(2)如图2,连接OD,
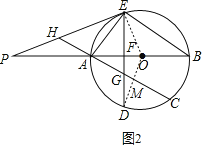
∵D为![]() 的中点,
的中点,
∴OD⊥AC,设垂足为M,
∴∠AMO=90°,
∵DE⊥AB,
∴∠AFD=90°,
∴∠AOD+∠OAM=∠OAM+∠AGF=90°,
∴∠AOD=∠AGF,
∵∠AEB=∠EFB=90°,
∴∠B=∠AEF,
∵∠PEA=∠B,
∴∠PEF=2∠B,
∵DE⊥AB,
∴![]() ,
,
∴∠AOD=2∠B,
∴∠PEF=∠AOD=∠AGF,
∴HE=HG;
(3)解:如图3,
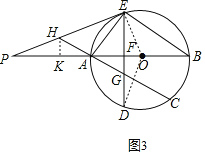
∵∠PEF=∠AOD,∠PFE=∠DFO,
∴∠P=∠ODF,
∴tan∠P=tan∠ODF=![]() ,
,
设OF=5x,则DF=12x,
∴OD=![]() =13x,
=13x,
∴BF=OF+OB=5x+13x=18x,AF=OA﹣OF=13x﹣5x=8x,
∵DE⊥OA,
∴EF=DF=12x,
∴AE=![]() =4
=4![]() x,BE=
x,BE=![]() =6
=6![]() x,
x,
∵∠PEA=∠B,∠EPA=∠BPE,
∴△PEA∽△PBE,
∴![]() ,
,
∵∠P+∠PEF=∠FAG+∠AGF=90°,
∴∠HEG=∠HGE,
∴∠P=∠FAG,
又∵∠FAG=∠PAH,
∴∠P=∠PAH,
∴PH=AH,
过点H作HK⊥PA于点K,
∴PK=AK,
∴![]() ,
,
∵tan∠P=![]() ,
,
设HK=5a,PK=12a,
∴PH=13a,
∴AH=13a,PE=36a,
∴HE=HG=36a﹣13a=23a,
∴AG=GH﹣AH=23a﹣13a=10a,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂长
的等腰直角三角形,摆动臂长![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
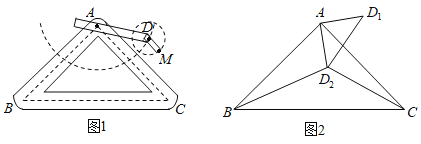
(1)在旋转过程中:
①当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的长;
的长;
②当![]() 三点在同一直角三角形的顶点时,求
三点在同一直角三角形的顶点时,求![]() 的长.
的长.
(2)若摆动臂![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
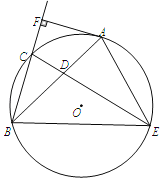
【题目】如图,已知AB是⊙O的弦,点C是弧AB的中点,D是弦AB上一动点,且不与A、B重合,CD的延长线交于⊙O点E,连接AE、BE,过点A作AF⊥BC,垂足为F,∠ABC=30°.
(1)求证:AF是⊙O的切线;
(2)若BC=6,CD=3,则DE的长为 ;
(3)当点D在弦AB上运动时,![]() 的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
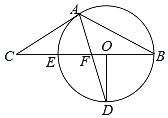
【题目】如图,在△ABC中,AC=AB,点E在BC上,以BE为直径的⊙O经过点A,点D是直径BE下方半圆的中点,AD交BC于点F,且∠B=2∠D.
(1)求∠B的度数;
(2)求证:AC为⊙O的切线;
(3)连接DE,若OD=3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
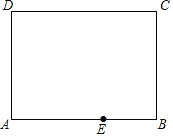
【题目】如图是一张矩形纸片ABCD,已知AB=8,AD=6,E为AB上一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在矩形ABCD的某一条边上,则等腰三角形AEP的底边上的高的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求一次函数的解析式和点![]() 的坐标;
的坐标;
(2)在反比例函数![]() 的图象上取一点
的图象上取一点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,若点
,若点![]() 恰为线段
恰为线段![]() 的中点,求点
的中点,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
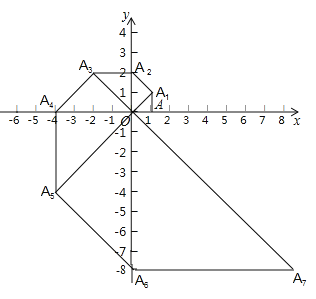
【题目】如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,OA1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2020的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的安全意识,某校组织了次“安全如识”测试,阅卷后,校团委随机抽取了部分学生的考卷进行了分析统计,发现测试成绩![]() (分)的最低分为60分.最高分为满分100分.并绘制了如下不完整的统计图表:
(分)的最低分为60分.最高分为满分100分.并绘制了如下不完整的统计图表:
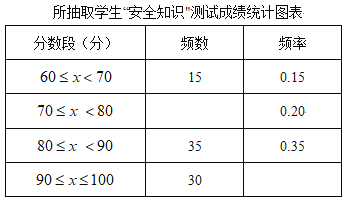
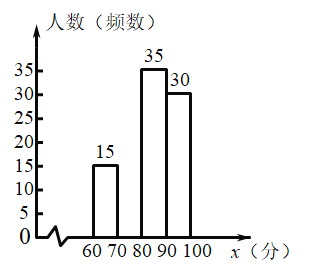
根据以上信息,解答下列问题:
(1)补全上面的统计图表;
(2)所抽取学生的测试成绩的中位数落在__________分数段内;
(3)已知该校共有2000名学生参加本次“安全知识”测试,请估计该校有多少名学生的测试成绩不低于80分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解全国中学生视力的情况,应采用普查的方式
B.某种彩票中奖的概率是![]() ,买1000张这种彩票一定会中奖
,买1000张这种彩票一定会中奖
C.从2000名学生中随机抽取200名学生进行调查,样本容量为200名学生
D.从只装有白球和绿球的袋中任意摸出一个球,摸出黑球是确定事件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com