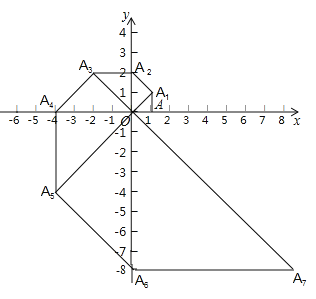
【题目】如图，在平面直角坐标系中，等腰直角三角形OAA1的直角边OA在x轴上，点A1在第一象限，且OA=1，以点A1为直角顶点，OA1为一直角边作等腰直角三角形OA1A2，再以点A2为直角顶点，OA2为直角边作等腰直角三角形OA2A3…依此规律，则点A2020的坐标是_________．
科目：初中数学 来源： 题型：
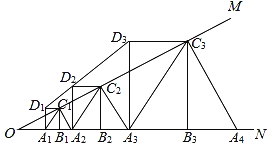
【题目】如图，∠MON＝30°，点A1在ON上，点C1在OM上，OA1＝A1C1＝2，C1B1⊥ON于点B1，以A1B1和B1C1为邻边作矩形A1B1C1D1，点A1，A2关于点B对称，A2C2∥A1C1交OM于点C2，C2B2⊥ON于点B2，以A2B2和B2C2为邻边作矩形A2B2C2D2，连接D1D2，点A2，A3关于点B2对称，A3C3∥A2C2交OM于点C3，C3B3⊥ON于点B3，以A3B3和B3C3为邻边作矩形A3B3C3D3，连接D2D3，……依此规律继续下去，则DnDn+1＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
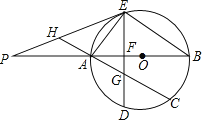
【题目】如图，已知AB是⊙O的直径，C是⊙O上一点（不与A、B重合），D为的
中点，过点D作弦DE⊥AB于F，P是BA延长线上一点，且∠PEA＝∠B．
（1）求证：PE是⊙O的切线；
（2）连接CA与DE相交于点G，CA的延长线交PE于H，求证：HE＝HG；
（3）若tan∠P＝
，试求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
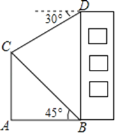
【题目】如图，楼房BD的前方竖立着旗杆AC．小亮在B处观察旗杆顶端C的仰角为45°，在D处观察旗杆顶端C的俯角为30°，楼高BD为20米．
（1）求∠BCD的度数；
（2）求旗杆AC的高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，正方形
与正方形
有公共的顶点
，连接
，
，
，
．
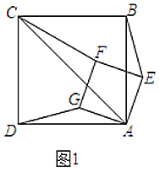
①求证：
；
②求
的值；
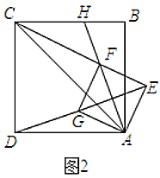
（2）将图1中的正方形旋转到图2的位置，当
，
，
在一条直线上，若
，求正方形的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案：一户家庭的月均用水量不超过
（单位：
）的部分按平价收费，超出的部分按议价收费．为此拟召开听证会，以确定一个合理的月均用水量标准．通过抽样，获得了前一年1000户家庭每户的月均用水量（单位：），将这1000个数据按照
，
，…，
分成8组，制成了如图所示的频数分布直方图．
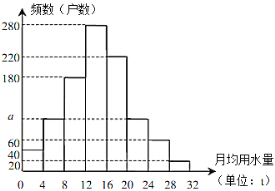
（1）写出
的值，并估计这1000户家庭月均用水量的平均数；（同一组中的数据以这组数据所在范围的组中值作代表）
（2）假定该市政府希望70%的家庭的月均用水量不超过标准，请判断若以（1）中所求得的平均数作为标准是否合理？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某社区计划对1200m2的区域进行绿化，经投标由甲、乙两个施工队来完成，已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍，并且甲、乙两队在分别独立完成面积为300m2区域的绿化时，甲队比乙队少用3天．
⑴ 甲、乙两施工队每天分别能完成绿化的面积是多少？
⑵ 设先由甲队施工x天，再由乙队施工y天，刚好完成绿化任务，求y关于x的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着时代的不断发展，新颖的网络购进逐渐融入到人们的生活中，“拼一拼”电商平台上提供了一种拼团购买方式，当拼团（单数不超过15单）成功后商家将会让利一定的额度给予顾客实惠．现在某商家准备出手一种每件成本25元/件的新产品，经市场调研发现，单价y（单位：元）、日销售量m（单位：件）与拼单数x（单位：单）之间存在着如表的数量关系：
拼单数x（单位：单） | 2 | 4 | 8 | 12 |
单价y（单位：元） | 34.50 | 34.00 | 33.00 | 32.00 |
日销售量m（单位：件） | 68 | 76 | 92 | 108 |
请根据以上提供的信息解决下列问题：
（1）请直接写出单价y和日销售量m分别与拼单数x之间的一次函数关系式；
（2）拼单数设置为多少单时的日销售利润最大，最大的销售利润是多少？
（3）在实际销售过程中，厂家希望能有更多的商品出售，因此对电商每销售一件商品厂家就给予电商补助a元（a≤2），那么电商在获得补助之日后日销售利润能够随单数x的增大而增大，那么a的取值范围是什么？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
