
分析 设二次函数的解析式为y=ax2+bx+c(a≠0),二次函数图象与x轴的两交点A、B坐标分别为(x1,0),(x2,0),根据二次函数图象与y轴交点的纵坐标为6得到c的值,再根据A、B的距离为8和△ABC的面积为32列出a和b的方程组,求出a和b的值,即可求出二次函数解析式.
解答 解:设二次函数的解析式为y=ax2+bx+c(a≠0),
二次函数图象与x轴的两交点A、B坐标分别为(x1,0),(x2,0),
∵二次函数图象与y轴交点的纵坐标为6,
∴c=6,
∵二次函数图象与x轴的两交点A、B的距离为8,
∴|x1-x2|=8,
∴$({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}$=64,
∴$\frac{{b}^{2}}{{a}^{2}}-\frac{24}{a}=64$①,
∵△ABC的面积为32,
∴$\frac{1}{2}$×8×|$\frac{24a-{b}^{2}}{4a}$|=32,
∴|$\frac{24a-{b}^{2}}{4a}$|=8②,
①②联立可得$\left\{\begin{array}{l}{{b}^{2}-24a=64{a}^{2}}\\{|\frac{24a-{b}^{2}}{4a}|=8}\end{array}\right.$,
解得a=±$\frac{1}{2}$,
当a=$\frac{1}{2}$时,4b2-48=64,
解得b=±2$\sqrt{7}$,
此时二次函数的解析式为y=$\frac{1}{2}$x2+2$\sqrt{7}$x+6或y=$\frac{1}{2}{x}^{2}$-2$\sqrt{7}$x+6,
当a=-$\frac{1}{2}$时,4b2+48=64,
解得b=±2,
此时二次函数的解析式为y=-$\frac{1}{2}$x2+2x+6或y=-$\frac{1}{2}{x}^{2}$-2x+6,
综上二次函数的解析式为y=$\frac{1}{2}$x2+2$\sqrt{7}$x+6或y=$\frac{1}{2}{x}^{2}$-2$\sqrt{7}$x+6或y=-$\frac{1}{2}$x2+2x+6或y=-$\frac{1}{2}{x}^{2}$-2x+6.
点评 本题主要考查了待定系数法求二次函数解析式的知识,解答本题的关键是根据题干条件列出a和b的方程组,此题答案不止一个,很容易漏解,此题有一定的难度.


科目:初中数学 来源: 题型:选择题
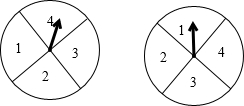 让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和概率最大的和等于( )
让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和概率最大的和等于( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
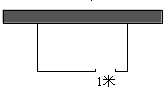 如图,有一长方形鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,竹篱笆的总长为35米,与墙平行的边留有1米宽的门(门用其它材料做成),若鸡场的面积为160平方米,则鸡场与墙垂直的边长为( )
如图,有一长方形鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,竹篱笆的总长为35米,与墙平行的边留有1米宽的门(门用其它材料做成),若鸡场的面积为160平方米,则鸡场与墙垂直的边长为( )| A. | 7.5米 | B. | 8米 | C. | 10米 | D. | 10米或8米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com