
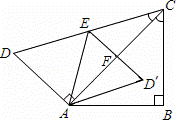
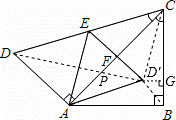
如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点.若AB=6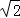 cm.
cm.
(1)AE的长为 cm;
(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;
(3)求点D′到BC的距离.
解:(1)∵∠BAC=45°,∠B=90°,
∴AB=BC=6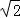 cm,
cm,
∴AC=12cm,
∵∠ACD=30°,∠DAC=90°,AC=12cm,
∴CD=AC÷cos30°=12÷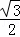 =12×
=12×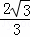 =8
=8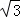 (cm),
(cm),
∵点E为CD边上的中点,
∴AE=DC=4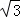 cm.
cm.
故答案为:4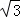 ;
;
(2)∵Rt△ADC中,∠ACD=30°,
∴∠ADC=60°,
∵E为CD边上的中点,
∴DE=AE,
∴△ADE为等边三角形,
∵将△ADE沿AE所在直线翻折得△AD′E,
∴△AD′E为等边三角形,
∠AED′=60°,
∵∠EAC=∠DAC﹣∠EAD=30°,
∴∠EFA=90°,
即AC所在的直线垂直平分线段ED′,
∴点E,D′关于直线AC对称,
连接DD′交AC于点P,
∴此时DP+EP值为最小,且DP+EP=DD′,
∵△ADE是等边三角形,AD=AE=4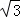 ,
,
∴DD′=2×AD×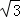 =2×6=12,
=2×6=12,
即DP+EP最小值为12cm;
(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,
∵AC垂直平分线ED′,
∴AE=AD′,CE=CD′,
∵AE=EC,∴AD′=CD′=4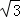 ,
,
在△ABD′和△CBD′中,
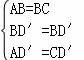 ,
,
∴△ABD′≌△CBD′(SSS),
∴∠D′BG=45°,
∴D′G=GB,
设D′G长为xcm,则CG长为(6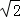 ﹣x)cm,
﹣x)cm,
在Rt△GD′C中
x2+(6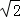 ﹣x)2=(4
﹣x)2=(4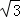 )2,
)2,
解得:x1=3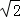 ﹣
﹣ ,x2=3
,x2=3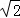 +
+ (不合题意舍去),
(不合题意舍去),
∴点D′到BC边的距离为(3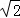 ﹣
﹣ )cm.
)cm.


科目:初中数学 来源: 题型:
已知反比例函数的图象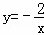 上有两点A(x1,y1)、B(x2,y2)
上有两点A(x1,y1)、B(x2,y2) ,若y1>y2,则x1﹣x2的值是( )
,若y1>y2,则x1﹣x2的值是( )
|
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某工厂一种产品2013年的产量是100万件,计划2015年产量达到121万件.假设2013年到2015年这种产品产量的年增长率相同.
(1)求2013年到2015年这种产品产量的年增长率;
(2)2014年这种产品的产量应达到多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
“六•一”期间,小洁的妈妈经营的玩具店进了一纸箱除颜色外都相同的散装塑料球共1000个,小洁将纸箱里面的球搅匀后,从中随机摸出一个球记下其颜色,把它放回纸箱中;搅匀后再随机摸出一个球记下其颜色,把它放回纸箱中;…多次重复上述过程后,发现摸到红球的频率逐渐稳定在0.2,由此可以估计纸箱内红球的个数约是 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
2014年12月26日,西南真正意义上的第一条高铁﹣贵阳至广州高速铁路将开始试运行,从贵阳到广州,乘特快列车的行程约为1800km,高铁开通后,高铁列车的行驶约为860km,运行时间比特快列车所用的时间减少了16h.若高铁列车的平均速度是特快列车平均速度的2.5倍,求特快列车的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com