
【题目】如图,在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与反比例函数
与反比例函数![]() 的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且
的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且![]() ⊥
⊥![]() .
.
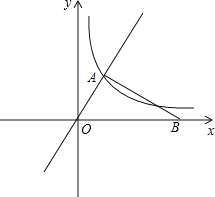
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在![]() 的内部求作点P,使点P到
的内部求作点P,使点P到![]() 的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)设点![]() 的坐标为(1,
的坐标为(1,![]() )先求出点A纵坐标,再求出反比例系数k即可得出反比例函数的解析式;
)先求出点A纵坐标,再求出反比例系数k即可得出反比例函数的解析式;
(2)过点A作AC⊥OB⊥,在RT△AOC中先求出OA,再在RT△AOB中求出OB即可解决问题;
(3)画出∠AOB的平分线OM,线段AB的垂直平分线EF,OM与EF的交点就是所求的点P,设点P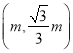 ,根据PA2=PB2,列出方程即可解决问题.
,根据PA2=PB2,列出方程即可解决问题.
解:(1)由题意,设点![]() 的坐标为(1,
的坐标为(1,![]() ),
),
∵点![]() 在正比例函数
在正比例函数![]() 的图像上,
的图像上,
∴![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
∵点![]() 在反比例函数
在反比例函数![]() 的图像上,
的图像上,
∴![]() ,解得
,解得![]() .
.
∴反比例函数的解析式为![]() .
.
(2)过点![]() 作
作![]() ⊥
⊥![]() ,垂足为点
,垂足为点![]() ,
,
可得![]() ,
,![]() .
.
∵![]() ⊥
⊥![]() ,
,
∴∠![]() °.
°.
由勾股定理,得![]() .
.
∴![]() .
.
∴∠![]() °.
°.
∴∠![]() °.
°.
∵![]() ⊥
⊥![]() ,
,
∴∠![]() °.
°.
∴∠![]() °.
°.
∴![]() .
.
∴![]() .
.
∴点![]() 的坐标是
的坐标是![]() .
.
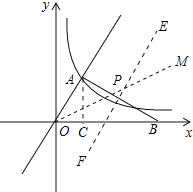
(3)如图所示.

如图作∠AOB的平分线OM,AB的垂直平分线EF,OM与EF的交点就是所求的点P,
∵∠POB=30°,
∴可以设点P坐标为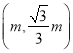 ,
,
∵PA2=PB2,
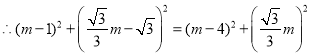
解得m=3,
∴点P的坐标是![]()


科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。

(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄河是中华民族的象征,被誉为母亲河,黄河壶口瀑布位于我省吉县城西45千米处,是黄河上最具气势的自然景观.其落差约30米,年平均流量1010立方米/秒.若以小时作时间单位,则其年平均流量可用科学记数法表示为( )

A. 6.06×104立方米/时 B. 3.136×106立方米/时
C. 3.636×106立方米/时 D. 36.36×105立方米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年1月20日,山西迎来了“复兴号”列车,与“和谐号”相比,“复兴号”列车时速更快,安全性更好.已知“太原南﹣北京西”全程大约500千米,“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米,其行驶时间是该列“和谐号”列车行驶时间的![]() (两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
(两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠BAC=90°,AB=AC,在△ABC外作∠ACM= ![]() ∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.

(1)①当点D在线段BC上时,如图1所示,求∠EDC的度数
②探究线段DF与EC的数量关系,并证明;
(2)当点D运动到CB延长线上时,请你画出图形,并证明此时DF与EC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
(1) ①依题意补全图形;②求证:BE⊥AC.
(2)设AB=1,若点M沿着线段CD从点C运动到点D,则在该运动过程中,线段EN所扫过的面积为 (直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D.
(1)求证:CD是⊙O的切线;
(2)E为![]() 的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=
的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=![]() ,BE=BG,EG=3
,BE=BG,EG=3![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
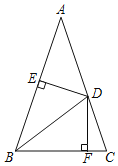
【题目】如图,△ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分別是E,F,下列结论:①BD是∠ABC的平分线;②D是AC的中点;③DE垂直平分AB;④AB=BC+CD;其中正确的结论是_____(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com