
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。

(1)判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
【答案】(1)直线PC与圆O相切(2)![]()
【解析】解:(1)直线PC与圆O相切。理由如下::
如图,连接CO并延长,交圆O于点N,连接BN,
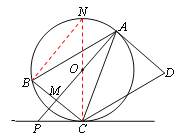
∵AB//CD,∴BAC=ACD。
∵BAC=BNC,∴BNC=ACD。
∵BCP=ACD,∴BNC=BCP。
∵CN是圆O的直径,∴CBN=90。
∴BNCBCN=90,∴BCPBCN=90。
∴PCO=90,即PCOC。
又∵点C在圆O上,∴直线PC与圆O相切。
(2)∵AD是圆O的切线,∴ADOA,即OAD=90。
∵BC//AD,∴OMC=180OAD=90,即OMBC。
∴MC=MB。∴AB=AC。
在Rt△AMC中,AMC=90,AC=AB=9,MC=![]() BC=3,
BC=3,
由勾股定理,得![]() 。
。
设圆O的半径为r,
在Rt△OMC中,OMC=90,OM=AMAO=![]() ,MC=3,OC=r,
,MC=3,OC=r,
由勾股定理,得OM 2MC 2=OC 2,即![]() 。解得
。解得![]() 。
。
在△OMC和△OCP中,∵OMC=OCP,MOC=COP,∴△OMC~△OCP。
∴![]() ,即
,即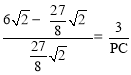 。∴
。∴![]() 。
。
(1)过C点作直径CE,连接EB,由CE为直径得∠E+∠BCE=90°,由AD∥BC得∠ACD=∠BAC,而
∠BAC=∠E,∠BCP=∠ACD,所以∠E=∠BCP,于是∠BCP+∠BCE=90°,然后根据切线的判断得到结论。
(2)根据切线的性质得到OA⊥AD,而BC∥AD,则AM⊥BC,根据垂径定理有BM=CM=![]() BC=3,根据线段垂直平分线的性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM=
BC=3,根据线段垂直平分线的性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM= ![]() 。设⊙O的半径为r,则OC=r,OM=AM-r=
。设⊙O的半径为r,则OC=r,OM=AM-r=![]() ,在Rt△OCM中,根据勾股定理计算出
,在Rt△OCM中,根据勾股定理计算出![]() ,从而由△OMC~△OCP得相似比可计算出PC。
,从而由△OMC~△OCP得相似比可计算出PC。


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
(1)求证:AD平分∠BAC;
(2)连接EF,求证:AD垂直平分EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汶川地震发生后,全国人民抗震救灾,众志成城某地政府急灾民之所需,立即组织![]() 辆汽车,将
辆汽车,将![]() 三种救灾物资共
三种救灾物资共![]() 吨一次性运往灾区,假设甲、乙,丙三种车型分别运载
吨一次性运往灾区,假设甲、乙,丙三种车型分别运载![]() 三种物资,根据下表提供的信息解答下列问题:
三种物资,根据下表提供的信息解答下列问题:
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) |
|
|
|
(1)设装运![]() 品种物资的车辆数分别为
品种物资的车辆数分别为![]() 试用含
试用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)据(1)中的表达式,试求![]() 三种物资各几吨.
三种物资各几吨.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,⊙O过AC的中点D,DE⊥BC,交BC于点E.
(1)求证:DE是⊙O的切线;
(2)如果CD=8,CE=6,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动,某读书小组随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、文艺类、科普类、其他等四类),并将调查结果绘制成如图所示的两幅不完整的统计图,请你结合图中的信息解答下列问题
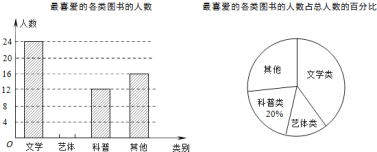
(1)被调查的学生人数为 人;
(2)科普类圆心角度数为 度,补全条形统计图;
(3)已知该校有1800名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
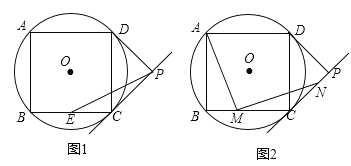
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列方程的特征及其解的特点.
①x+![]() =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+![]() =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+![]() =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为________,其解为________;
(2)根据这类方程的特征,写出第n个方程为________,其解为________;
(3)请利用(2)的结论,求关于x的方程x+![]() =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与反比例函数
与反比例函数![]() 的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且
的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且![]() ⊥
⊥![]() .
.
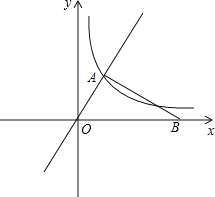
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在![]() 的内部求作点P,使点P到
的内部求作点P,使点P到![]() 的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com