
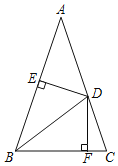
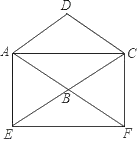
【题目】如图,△ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分別是E,F,下列结论:①BD是∠ABC的平分线;②D是AC的中点;③DE垂直平分AB;④AB=BC+CD;其中正确的结论是_____(填序号).
【答案】①③④
【解析】
根据等腰三角形的性质可得∠ABC=∠C=∠BDC=72°,利用外角性质可得∠ABD=36°,可得∠ABD=∠A=∠DBC=36°,根据等腰三角形的性质对各选项逐一判定即可得答案.
①∵∠A=36°,AB=AC,
∴∠ABC=∠C=72°,
∵BD=BC,
∴∠BDC=∠C=72°,
∵∠BDC=∠A+∠ABD,
∴∠ABD=36°,
∴∠ABD=∠CBD=36°,即BD是∠ABC的平分线,①正确.
②∵∠A+∠ABD=36°,
∴AD=BD,
∵BD≠CD,
∴AD≠CD,故②错误;
③∵∠ABD=∠A=36°,
∴AD=BD,
∵DE⊥AB,
∴AE=BE,
∴DE垂直平分AB,③正确;
④由①③可知,AD=BD=BC,
∵AB=AC,
∴AB=AD+CD=BC+CD,④正确;
综上所述,正确的结论有①③④,
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与反比例函数
与反比例函数![]() 的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且
的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且![]() ⊥
⊥![]() .
.
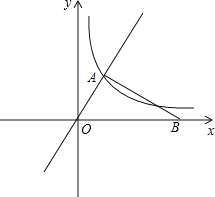
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在![]() 的内部求作点P,使点P到
的内部求作点P,使点P到![]() 的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=105°.
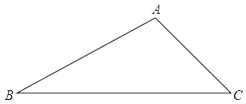
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到∠ABC两边的距离相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠BCP=15°,则∠ACB的度数为 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】益马高速通车后,将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A,B两种农产品定期运往益阳某加工厂,每次运输A,B产品的件数不变,原来每运一次的运费是1200元,现在每运一次的运费比原来减少了300元,A,B两种产品原来的运费和现在的运费(单位:元∕件)如下表所示:
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
(1)求每次运输的农产品中A,B产品各有多少件?
(2)由于该农户诚实守信,产品质量好,加工厂决定提高该农户的供货量,每次运送的总件数增加8件,但总件数中B产品的件数不得超过A产品件数的2倍,问产品件数增加后,每次运费最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3 m,沿BD方向行走到达G点,DG=5 m,这时大华的影长GH=4 m如果大华的身高为2 m,求路灯杆AB的高度.
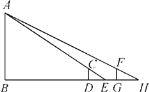
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,菱形ABCD,分别延长AB,CB到点F,E,使得BF=BA,BE=BC,连接AE,EF,FC,CA.
(1)求证:四边形AEFC为矩形;
(2)连接DE交AB于点O,如果DE⊥AB,AB=4,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com