
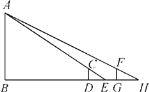
【题目】如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3 m,沿BD方向行走到达G点,DG=5 m,这时大华的影长GH=4 m如果大华的身高为2 m,求路灯杆AB的高度.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.直线y=﹣2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为﹣1.
(1)求点B的坐标及k的值;
(2)直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线,DE⊥AB,垂足为点E,DE=1,BE=![]() ,则△ABC的周长是( )
,则△ABC的周长是( )

A.6+![]() B.3+2
B.3+2![]() C.6+2
C.6+2![]() D.3+3
D.3+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
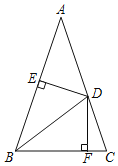
【题目】如图,△ABC中,AB=AC,∠A=36°,D是AC上一点,且BD=BC,过点D分别作DE⊥AB,DF⊥BC,垂足分別是E,F,下列结论:①BD是∠ABC的平分线;②D是AC的中点;③DE垂直平分AB;④AB=BC+CD;其中正确的结论是_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
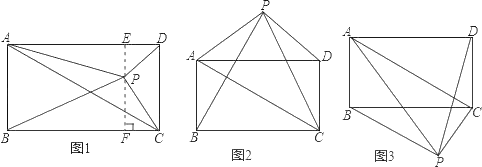
【题目】已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+S△PCD
理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵S△PBC+S△PAD=![]() BCPF+
BCPF+![]() ADPE=
ADPE=![]() BC(PF+PE)=
BC(PF+PE)=![]() BCEF=
BCEF=![]() S矩形ABCD.
S矩形ABCD.
(1)请补全以上证明过程.
(2)请你参考上述信息,当点P分别在图1、图2中的位置时,S△PBC、S△PAC、SPCD又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,已知点A(﹣3,﹣3),点B(﹣1,﹣3),点C(﹣1,﹣1).
(1)画出△ABC;
(2)画出△ABC关于x轴对称的△A1B1C1,并写出A1点的坐标: ;
(3)以O为位似中心,在第一象限内把△ABC扩大到原来的两倍,得到△A2B2C2,并写出A2点的坐标: .

查看答案和解析>>
科目:初中数学 来源: 题型:
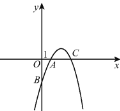
【题目】如图,抛物线y=-x2+5x+n与x轴交于点A(1,0)和点C,与y轴交于点B.
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com