
【题目】在如图所示的平面直角坐标系中,已知点A(﹣3,﹣3),点B(﹣1,﹣3),点C(﹣1,﹣1).
(1)画出△ABC;
(2)画出△ABC关于x轴对称的△A1B1C1,并写出A1点的坐标: ;
(3)以O为位似中心,在第一象限内把△ABC扩大到原来的两倍,得到△A2B2C2,并写出A2点的坐标: .

科目:初中数学 来源: 题型:
【题目】甘肃省省府兰州,又名金城,在金城,黄河母亲河通过自身文化的演绎,衍生和流传了独特的“金城八宝”美食,“金城八宝”美食中甜品类有:味甜汤糊“灰豆子”、醇香软糯“甜胚子”、生津润肺“热冬果”、香甜什锦“八宝百合”;其他类有:青白红绿“牛肉面”、酸辣清凉“酿皮子”、清爽溜滑“浆水面”、香醇肥美“手抓羊肉”,李华和王涛同时去品尝美食,李华准备在“甜胚子、牛肉面、酿皮子、手抓羊肉”这四种美食中选择一种,王涛准备在“八宝百合、灰豆子、热冬果、浆水面”这四种美食中选择一种。(甜胚子、牛肉面、酿皮子、手抓羊肉分别记为A、B、C、D;八宝百合、灰豆子、热冬果、浆水面分别记为E、F、G、H)
(1)用树状图或表格的方法表示李华和王涛同时选择美食的所有可能结果;
(2)求李华和王涛同时选择的美食都是甜品类的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
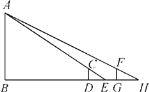
【题目】如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3 m,沿BD方向行走到达G点,DG=5 m,这时大华的影长GH=4 m如果大华的身高为2 m,求路灯杆AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边AB在数轴上,数轴上点A表示的数为-1,正方形ABCD的面积为16.
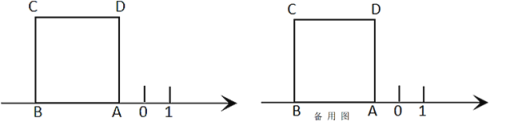
(1)数轴上点B表示的数为___;
(2)将正方形ABCD沿数轴水平移动,移动后的正方形记为A′B′C′D′,移动后的正方形A′B′C′D′与原正方形ABCD重叠部分的面积为S.
①当S=4时,画出图形,并求出数轴上点A′表示的数;
②设正方形ABCD的移动速度为每秒2个单位长度,点E为线段AA′的中点,点F在线段BB′上,且BF=![]() BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值.
BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,直线L和直线AB,CD分别交于点E,F,直线L上有一动点P.

(1)如图1,点P在E,F之间运动时,∠PMB,∠MPN,∠PND之间有什么关系,并说明理由;
(2)若点P在E,F两点外侧运动时,如图2和图3(P点与E,F不重合),试直接写出∠PMB,∠MPN,∠PND之间有什么关系,不必写理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
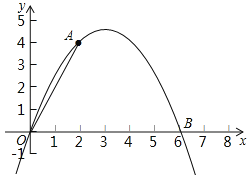
【题目】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探索三角形全等的条件时,老师给出了定长线段![]() ,且长度为
,且长度为![]() 的边所对的角为
的边所对的角为![]() 小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中
小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中![]() 发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:
发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:


(1)当![]() 时(如图2),小明测得
时(如图2),小明测得![]() ,请根据小明的测量结果,求
,请根据小明的测量结果,求![]() 的大小;
的大小;
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() (如图3),小明和小亮发现
(如图3),小明和小亮发现![]() 的大小与角度
的大小与角度![]() 有关,请找出它们的关系,并说明理由;
有关,请找出它们的关系,并说明理由;
(3)如图4,在(2)问的基础上,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com