
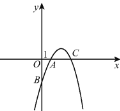
【题目】如图,抛物线y=-x2+5x+n与x轴交于点A(1,0)和点C,与y轴交于点B.
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.
【答案】(1) y=-x2+5x-4 ;(2)6;(3) P的坐标为(0,![]() -4)或(0,-
-4)或(0,-![]() -4)或(0,4).
-4)或(0,4).
【解析】
(1)将点A的坐标代入抛物线中,即可得出二次函数的解析式;(2)求得点B、C的坐标,根据三角形的面积公式求解即可;(3)分PB=AB和PA=AB两种情况求点P的坐标即可.
解:(1)根据题意,得0=-1+5+n,解得n=-4,
∴抛物线的解析式为y=-x2+5x-4.
(2)令y=0,即-x2+5x-4=0,解得x1=1,x2=4,
∴点C坐标为(4,0).
令x=0,解得y=-4,∴点B的坐标为(0,-4).
∴由图象可得S△ABC=![]() ×OB×AC=
×OB×AC=![]() ×4×3=6.
×4×3=6.
(3)①当PA=AB时,则点O为PB的中点,
∴OP=OB=4,
∴点P的坐标为(0,4);
②当AB=BP时,AB=![]() ,
,
∴OP=![]() ±4,∴点P的坐标为(0,
±4,∴点P的坐标为(0,![]() -4)或(0,-
-4)或(0,-![]() -4).
-4).
综上,点P的坐标为(0,![]() -4)或(0,-
-4)或(0,-![]() -4)或(0,4).
-4)或(0,4).


科目:初中数学 来源: 题型:
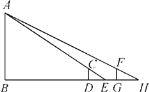
【题目】如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3 m,沿BD方向行走到达G点,DG=5 m,这时大华的影长GH=4 m如果大华的身高为2 m,求路灯杆AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,直线L和直线AB,CD分别交于点E,F,直线L上有一动点P.

(1)如图1,点P在E,F之间运动时,∠PMB,∠MPN,∠PND之间有什么关系,并说明理由;
(2)若点P在E,F两点外侧运动时,如图2和图3(P点与E,F不重合),试直接写出∠PMB,∠MPN,∠PND之间有什么关系,不必写理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
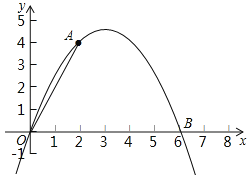
【题目】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式![]() ,........请按照上述三个等式及其变化过程,回答下列问题。
,........请按照上述三个等式及其变化过程,回答下列问题。
(1)猜想![]() ________________.
________________.
(2)猜想_____________________=![]() .
.
(3)试猜想第N个等式为_____________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
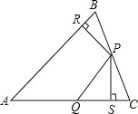
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是( ).
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在探索三角形全等的条件时,老师给出了定长线段![]() ,且长度为
,且长度为![]() 的边所对的角为
的边所对的角为![]() 小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中
小明和小亮按照所给条件分别画出了图1中的三角形,他们把两个三角形重合在一起(如图2),其中![]() 发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:
发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究:


(1)当![]() 时(如图2),小明测得
时(如图2),小明测得![]() ,请根据小明的测量结果,求
,请根据小明的测量结果,求![]() 的大小;
的大小;
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() (如图3),小明和小亮发现
(如图3),小明和小亮发现![]() 的大小与角度
的大小与角度![]() 有关,请找出它们的关系,并说明理由;
有关,请找出它们的关系,并说明理由;
(3)如图4,在(2)问的基础上,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,∠ABG为锐角,AH∥BG,点C从点B(C不与B重合)出发,沿射线BG的方向移动,CD∥AB交直线AH于点D,CE⊥CD交AB于点E,CF⊥AD,垂足为F(F不与A重合),若∠ECF=n°,则∠BAF的度数为_____度.(用n来表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com