
【题目】如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是( ).
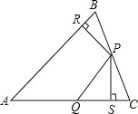
A.①②B.①②③C.①②④D.①②③④
【答案】C
【解析】
如图,连接AP,根据HL判定△APR和△APS全等,即可说明①正确;由△APR和△APS全等可得∠RAP=∠PAC,再根据等腰三角形性质推出∠QAP=∠QPA,得到∠QPA=∠BAP,根据平行线判定推出OP//AB,即②正确;在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等;连接RS,与AP交于点D,先证△ARD≌△ASD,即RD=SD;运用等腰三角形的性质即可判定.
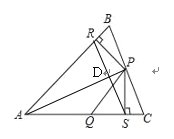
解:如图,连接AP
∵PR⊥AB,PS⊥AC,PR=PS
∴△APR≌△APS
∴AS=AR,∠RAP=∠PAC
即①正确;
又∵AQ=PQ
∴∠QAP=∠QPA
∴∠QPA=∠BAP
∴OP//AB,即②正确.
在Rt△BRP和Rt△QSP中,只有PR=PS.无法判断Rt△BRP和Rt△QSP是否全等,故③错误.
如图,连接PS
∵△APR≌△APS
∴AR=AS,∠RAP=∠PAC
∴AP垂直平分RS,即④正确;
故答案为C.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
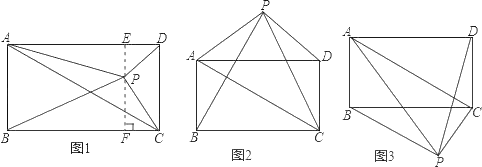
【题目】已知矩形ABCD和点P,当点P在图1中的位置时,则有结论:S△PBC=S△PAC+S△PCD
理由:过点P作EF垂直BC,分别交AD、BC于E、F两点.
∵S△PBC+S△PAD=![]() BCPF+
BCPF+![]() ADPE=
ADPE=![]() BC(PF+PE)=
BC(PF+PE)=![]() BCEF=
BCEF=![]() S矩形ABCD.
S矩形ABCD.
(1)请补全以上证明过程.
(2)请你参考上述信息,当点P分别在图1、图2中的位置时,S△PBC、S△PAC、SPCD又有怎样的数量关系?请写出你对上述两种情况的猜想,并选择其中一种情况的猜想给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:①y=2x2-3xz+5;②y=3-2x+5x2;③y=![]() +2x-3;④y=ax2+bx+c;⑤y=(2x-3)(3x-2)-6x2;⑥y=(m2+1)x2+3x-4(m为常数);⑦y=m2x2+4x-3(m为常数)是二次函数的有( )
+2x-3;④y=ax2+bx+c;⑤y=(2x-3)(3x-2)-6x2;⑥y=(m2+1)x2+3x-4(m为常数);⑦y=m2x2+4x-3(m为常数)是二次函数的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
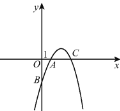
【题目】如图,抛物线y=-x2+5x+n与x轴交于点A(1,0)和点C,与y轴交于点B.
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点D是AB的中点,连结CD,过点B作BG⊥CE,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下五个结论:
,点D是AB的中点,连结CD,过点B作BG⊥CE,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下五个结论:
①![]() ;②
;②![]() ;③点F是GE的中点;④
;③点F是GE的中点;④![]() ;⑤
;⑤![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是请给出证明,
(3)在(2)的条件下,求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比S△ADE∶S△ABC∶ S△AMN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,
他的结论是 (直接写结论,不需证明);
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的二分之一,上述结论是否仍然成立,并说明理由.
(3)如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出三角形DEF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
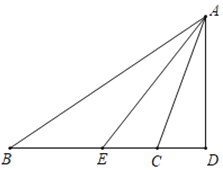
【题目】如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,E为BC延长线上一点.
(1)请你添加平行线证明:∠ACE=∠ABC+∠A.
(2)如图2,若点D是线段AC上一点,且DF∥BC,作DG平分∠BDF交AB于G,DH平分∠GDC交BC于H,且∠BDC比∠ACB大20°,求∠GDH的度数.
(3)如图3,已知E为BC延长线上一点,D是线段AC上一点,连接DE,若∠ABC的平分线与∠ADE的平分线相交于点P,请你判断∠P、∠A、∠E的数量关系并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com