【题目】下列各式:①y=2x2-3xz+5;②y=3-2x+5x2;③y=
+2x-3;④y=ax2+bx+c;⑤y=(2x-3)(3x-2)-6x2;⑥y=(m2+1)x2+3x-4(m为常数);⑦y=m2x2+4x-3(m为常数)是二次函数的有( )
A. 1个 B. 2个 C. 3个 D. 4个
全优考典单元检测卷及归类总复习系列答案科目：初中数学 来源： 题型：
【题目】益马高速通车后，将桃江马迹塘的农产品运往益阳的运输成本大大降低。马迹塘一农户需要将A，B两种农产品定期运往益阳某加工厂，每次运输A，B产品的件数不变，原来每运一次的运费是1200元，现在每运一次的运费比原来减少了300元，A，B两种产品原来的运费和现在的运费（单位：元∕件）如下表所示：
品种 | A | B |
原来的运费 | 45 | 25 |
现在的运费 | 30 | 20 |
（1）求每次运输的农产品中A，B产品各有多少件？
（2）由于该农户诚实守信，产品质量好，加工厂决定提高该农户的供货量，每次运送的总件数增加8件，但总件数中B产品的件数不得超过A产品件数的2倍，问产品件数增加后，每次运费最少需要多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线AB∥CD，直线L和直线AB，CD分别交于点E，F，直线L上有一动点P．
（1）如图1，点P在E，F之间运动时，∠PMB，∠MPN，∠PND之间有什么关系，并说明理由；
（2）若点P在E，F两点外侧运动时，如图2和图3（P点与E，F不重合），试直接写出∠PMB，∠MPN，∠PND之间有什么关系，不必写理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠B=90°，点P从点A开始沿AB边向点B以1㎝/秒的速度移动，同时点Q从点B开始沿BC边向点C以2㎝/秒的速度移动．（
）
（1）如果ts秒时，PQ//AC,请计算t的值.
（2）如果ts秒时，△PBQ的面积等于S㎝2，用含t的代数式表示S．
（3）PQ能否平分△ABC的周长？如果能，请计算出t值，不能，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
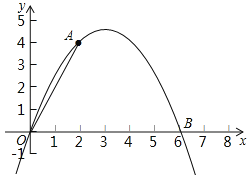
【题目】如图，二次函数y=ax2+bx的图象经过点A（2，4）与B（6，0）．
（1）求a，b的值；
（2）点C是该二次函数图象上A，B两点之间的一动点，横坐标为x（2＜x＜6），写出四边形OACB的面积S关于点C的横坐标x的函数表达式，并求S的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别是R、S，若AQ=PQ，PR=PS，下面四个结论：①AS=AR；②QP∥AR；③△BRP≌△QSP；④AP垂直平分RS．其中正确结论的序号是（ ）．
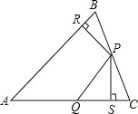
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题：如图①，在直角三角形
中，
，
于点
，可知
（不需要证明）；
（1）探究：如图②，
，射线
在这个角的内部，点
、
在
的边
、
上，且
，
于点
，
于点．证明：
；
（2）证明：如图③，点、在的边、上，点
、在内部的射线
上，
、
分别是
、
的外角。已知，
．求证：
；
（3）应用：如图④，在
中，，
．点在边
上，
，点、在线段上，．若的面积为15，则
与
的面积之和为________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
