
【题目】问题:如图①,在直角三角形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,可知
,可知![]() (不需要证明);
(不需要证明);
(1)探究:如图②,![]() ,射线
,射线![]() 在这个角的内部,点
在这个角的内部,点![]() 、
、![]() 在
在![]() 的边
的边![]() 、
、![]() 上,且
上,且![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .证明:
.证明:![]() ;
;
(2)证明:如图③,点![]() 、
、![]() 在
在![]() 的边
的边![]() 、
、![]() 上,点
上,点![]() 、
、![]() 在
在![]() 内部的射线
内部的射线![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的外角。已知
的外角。已知![]() ,
,![]() .求证:
.求证:![]() ;
;
(3)应用:如图④,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .若
.若![]() 的面积为15,则
的面积为15,则![]() 与
与![]() 的面积之和为________.
的面积之和为________.

【答案】(1)见解析;(2)见解析;(3)5.
【解析】
(1)利用AAS证明即可;
(2)利用AAS证明即可;
(3)先利用AAS证明△ABE≌△CAF,然后求△ABD的面积即可.
解:(1)∵![]() ,
,![]() ,
,![]()
∴![]()
∴∠DBA+∠BAD=90°,∠BAD+∠FAC=90°
∴∠DBA=∠FAC
在△ABD和△CAF中,

∴![]()
 ;
;
(2)∵![]() ,∠1=∠EBA+∠EAB,∠BAC=∠EAB+∠FAC
,∠1=∠EBA+∠EAB,∠BAC=∠EAB+∠FAC
∴∠BEA=180°-∠1=180°-∠2=∠AFC,∠EBA=∠FAC
在△ABE和△CAF中

∴![]() .
.
 ;
;
(3)∵![]() ,∠1=∠EBA+∠EAB,∠BAC=∠EAB+∠FAC
,∠1=∠EBA+∠EAB,∠BAC=∠EAB+∠FAC
∴∠BEA=180°-∠1=180°-∠2=∠AFC,∠EBA=∠FAC
在△ABE和△CAF中

∴![]()

∴△ABE的面积=△CAF的面积
∵![]()
∴![]()
∴![]()
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列各式:①y=2x2-3xz+5;②y=3-2x+5x2;③y=![]() +2x-3;④y=ax2+bx+c;⑤y=(2x-3)(3x-2)-6x2;⑥y=(m2+1)x2+3x-4(m为常数);⑦y=m2x2+4x-3(m为常数)是二次函数的有( )
+2x-3;④y=ax2+bx+c;⑤y=(2x-3)(3x-2)-6x2;⑥y=(m2+1)x2+3x-4(m为常数);⑦y=m2x2+4x-3(m为常数)是二次函数的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段EF,BE,FD之间的数量关系.
小明同学探究的方法是:延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,
他的结论是 (直接写结论,不需证明);
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF是∠BAD的二分之一,上述结论是否仍然成立,并说明理由.
(3)如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出三角形DEF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD.
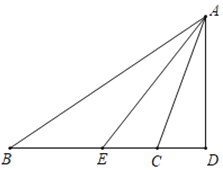
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,已知线段AD平分∠BAC交BC于D,∠B=62°,∠C=58°.
(1)用尺规作出线段AD,并求∠ADB的度数;
(2)若DE⊥AC于点E,把图形补充完整并求∠ADE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形的纸片ABCD中,AD=3cm,AB=4cm,把该纸片沿直线AC折叠,点B落在点E处,AE交DC于点F.
(1)图中有等腰三角形吗?说明理由.
(2)求重叠部分(即△ACF)的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,E为BC延长线上一点.
(1)请你添加平行线证明:∠ACE=∠ABC+∠A.
(2)如图2,若点D是线段AC上一点,且DF∥BC,作DG平分∠BDF交AB于G,DH平分∠GDC交BC于H,且∠BDC比∠ACB大20°,求∠GDH的度数.
(3)如图3,已知E为BC延长线上一点,D是线段AC上一点,连接DE,若∠ABC的平分线与∠ADE的平分线相交于点P,请你判断∠P、∠A、∠E的数量关系并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com