
【题目】如图,已知关于x的一元二次方程x2+2x+![]() =0有两个不相等的实数根,k为正整数.
=0有两个不相等的实数根,k为正整数.
(1)求k的值;
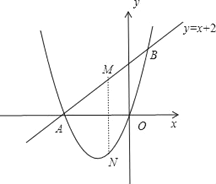
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+![]() 的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.
的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.
【答案】(1)k=1或2;(2)当t=﹣![]() 时,MN有最大值,最大值为
时,MN有最大值,最大值为![]() .
.
【解析】
(1)、根据方程有两个不相等的实数根得出△>0,从而得出k的取值范围,然后根据k为正整数,从而得出k的值;(2)、将x=0代入方程求出k的值,从而得出函数解析式,解出函数的交点坐标,设M(t,t+2)(﹣2<t<1),则N(t,t2+2t),然后根据长度的计算法则得出函数解析式,从而得出最大值.
(1)根据题意得△=22﹣4×![]() >0,解得k<3,而k为正整数, 所以k=1或2;
>0,解得k<3,而k为正整数, 所以k=1或2;
(2)当x=0代入x2+2x+![]() =0得k=1,则方程为x2+2x=0, 二次函数为y=x2+2x,
=0得k=1,则方程为x2+2x=0, 二次函数为y=x2+2x,
解方程组![]() 得
得![]() 或
或![]() ,则A(﹣2,0),B(1,3),
,则A(﹣2,0),B(1,3),
设M(t,t+2)(﹣2<t<1),则N(t,t2+2t),
所以MN=t+2﹣(t2+2t)=﹣t2﹣t+2=﹣(t+![]() )2+
)2+![]() ,
,
当t=﹣![]() 时,MN有最大值,最大值为
时,MN有最大值,最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
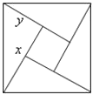
【题目】如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=![]() .其中说法正确的结论有_______.(填序号)
.其中说法正确的结论有_______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
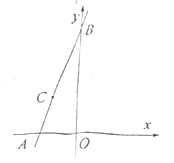
【题目】在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于点
轴于点![]() .
.
(1)当![]() ,自变量
,自变量![]() 的取值范围是 (直接写出结果);
的取值范围是 (直接写出结果);
(2)点![]() 在直线
在直线![]() 上.
上.
①直接写出![]() 的值为 ;
的值为 ;
②过![]() 点作
点作![]() 交
交![]() 轴于点
轴于点![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )

A. (1)(2)(3)(4) B. (2)(4)(5) C. (2)(3)(4) D. (1)(4)(5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
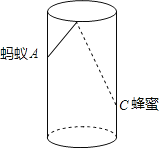
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com