
【题目】(思考)
如果x1,x2是一元二次方程ax2+bx+c=0的两根,那么有x1+x2=﹣![]() ,x1x2=
,x1x2=![]() ,这是一元二次方程根与系数的关系,我们可以利用它来解决问题
,这是一元二次方程根与系数的关系,我们可以利用它来解决问题
(应用)
(1)若x1,x2是方程x2+x﹣1=0的两根,则x1+x2= x1x2= ,求![]() 的值.
的值.
(2)关于x的一元二次方程kx2+(k﹣3)x+![]() =0有两个不相等的实数根为x1,x2,且满足x1x2﹣2(x1+x2)+4=2k﹣
=0有两个不相等的实数根为x1,x2,且满足x1x2﹣2(x1+x2)+4=2k﹣![]() ,请考虑k的取值范围前提下,求出k的值
,请考虑k的取值范围前提下,求出k的值
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
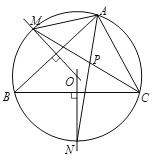
【题目】如图,在![]() 中,
中,
(1)作AB和BC的垂直平分线交于点O;
(2)以点O为圆心,OA长为半径作圆;
(3)⊙O分别与AB和BC的垂直平分线交于点M,N;
(4)连接AM,AN,CM,其中AN与CM交于点P.
根据以上作图过程及所作图形,下列四个结论中,
①![]() ; ②
; ②![]() ;
;
③点O是![]() 的外心 ; ④点P是
的外心 ; ④点P是![]() 的内心.
的内心.
所有正确结论的序号是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的对称轴为x=﹣1,且过点(﹣3,0),(0,﹣3).
(1)求抛物线的表达式.
(2)已知点(m,k)和点(n,k)在此抛物线上,其中m≠n,请判断关于t的方程t2+mt+n=0是否有实数根,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
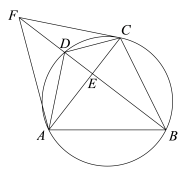
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
某生态示范园要对1号、2号、3号、4号四个新品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知:3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).

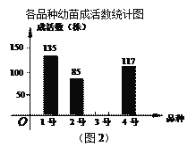
(1)实验所用的2号果树幼苗的数量是_______株;
(2)求出3号果树幼苗的成活数,并把图2的统计图补充完整;
(3)你认为应选哪一种果树幼苗进行推广?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() :
:![]() 与x轴、y轴分别交于A、R两点,直线
与x轴、y轴分别交于A、R两点,直线![]() 与x轴、y轴分别交于C、
与x轴、y轴分别交于C、![]() 两点,且
两点,且![]() ︰
︰![]() ︰
︰![]() .
.
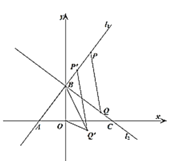

(1)如图![]() ,
,![]() 为直线
为直线![]() 上一点,横坐标为
上一点,横坐标为![]() ,
,![]() 为直线
为直线![]() 上一动点,当
上一动点,当![]() 最小时,将线段
最小时,将线段![]() 沿射线
沿射线![]() 方向平移,平移后
方向平移,平移后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,当
,当![]() 最小时,求点
最小时,求点![]() 的坐标;
的坐标;
(2)如图![]() ,将
,将![]() 沿着
沿着![]() 轴翻折,得到
轴翻折,得到![]() ,再将
,再将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() (
(![]() )得到
)得到![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .当
.当![]() 为等腰三角形时,请直接写出线段
为等腰三角形时,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,BC=2.将△ABC绕点C逆时针旋转α角后得到△A′B′C,当点A的对应点A'落在AB边上时,旋转角α的度数是_____度,阴影部分的面积为_____.
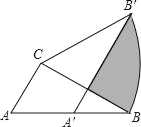
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com