
【题目】如图,直线![]() :
:![]() 与x轴、y轴分别交于A、R两点,直线
与x轴、y轴分别交于A、R两点,直线![]() 与x轴、y轴分别交于C、
与x轴、y轴分别交于C、![]() 两点,且
两点,且![]() ︰
︰![]() ︰
︰![]() .
.
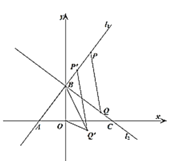

(1)如图![]() ,
,![]() 为直线
为直线![]() 上一点,横坐标为
上一点,横坐标为![]() ,
,![]() 为直线
为直线![]() 上一动点,当
上一动点,当![]() 最小时,将线段
最小时,将线段![]() 沿射线
沿射线![]() 方向平移,平移后
方向平移,平移后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,当
,当![]() 最小时,求点
最小时,求点![]() 的坐标;
的坐标;
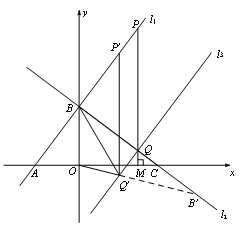
(2)如图![]() ,将
,将![]() 沿着
沿着![]() 轴翻折,得到
轴翻折,得到![]() ,再将
,再将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() (
(![]() )得到
)得到![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() .当
.当![]() 为等腰三角形时,请直接写出线段
为等腰三角形时,请直接写出线段![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2) ![]() 的长为:
的长为:![]() 或
或 ![]() 或
或![]() 或
或![]() .
.
【解析】
(1)如图,作QM⊥x轴于M,首先说明当P、Q、M三点共线,且PM⊥x轴时,![]() 最小,构建一次函数理由方程组确定交点Q的坐标即可;
最小,构建一次函数理由方程组确定交点Q的坐标即可;
(2)根据题意,可以分四种情形分别求解,即可解决问题;
解:(1)∵直线l1:![]() ,
,
∴A(-9,0),B(0,12),
∴在Rt△AOB中,AB=15,
∵AB:BC=3:4,
∴BC=20,
∴在Rt△BOC中,OC=16,
即C(16,0),
设直线l2:y=kx+b(k≠0),
∴![]() ,解得
,解得 ,
,
∴直线l2:![]() ,
,
作QM⊥x轴于M,
 ,
,
则△CQM∽△CBO.
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴当P、Q、M三点共线,且PM⊥x轴时,PQ+![]() CQ最小,
CQ最小,
∴Q(12,3),
平移过程中,点Q'在直线l3上移动,
∵l3∥l1且l3经过点Q(12,3),
∴l3:y=![]() x13,
x13,
作点B(0,12)关于l3的对称点B',则B'
∵直线OB':y=![]() x,
x,
∴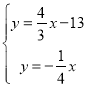 ,解得
,解得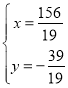 ,
,
∴点Q’的坐标为:![]() .
.
(2)①如图2中,当AN=AM时,作AG⊥MN于G,易知AG=![]() ,
,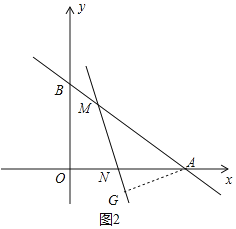
∵∠MAN=∠NMA,
∴sin∠AMN=sin∠BAO=![]() ,
,
∴![]() ,
,
∴AM=![]() ,
,
∴BM=AB-AM=![]() ;
;
②如图2中,当AN=AM时,作AG⊥MN于G,延长AG交OB于K,作KT⊥AB于T.
∵AM=AN,AG⊥MN,
∴∠GAM=∠GAN,
∴KO=KT,设KO=KT=m,
∵△AKO≌△AKT,
∴OA=AT=16,BT=AB-AT=4,
在Rt△BKT中,(12-m)2=m2+42,
∴m=![]() ,
,
在Rt△AKO中,AK=![]() ,
,
∵cos∠GAM=![]() ,
,
∴ ,
,
∴![]() ,
,
∴![]() ;
;
③如图4中,当AM=MN时,
∵tan∠MNA=tan∠MAN=![]() ,
,
∴GN=![]() ,设AM=MN=n,
,设AM=MN=n,
在Rt△AGN中,可得n2=(![]() -n)2+(
-n)2+(![]() )2,
)2,
解得n=![]() ,
,
∴BM=AB=AM=![]() ;
;
④如图5中,当AM=AN时,
由②可知,sin∠GAM=![]() ,
,
∴![]() ,
,
∴BM=![]() ;
;
综合上述,![]() 的长为:
的长为:![]() 或
或 ![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.
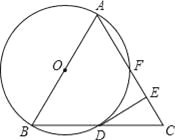
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(思考)
如果x1,x2是一元二次方程ax2+bx+c=0的两根,那么有x1+x2=﹣![]() ,x1x2=
,x1x2=![]() ,这是一元二次方程根与系数的关系,我们可以利用它来解决问题
,这是一元二次方程根与系数的关系,我们可以利用它来解决问题
(应用)
(1)若x1,x2是方程x2+x﹣1=0的两根,则x1+x2= x1x2= ,求![]() 的值.
的值.
(2)关于x的一元二次方程kx2+(k﹣3)x+![]() =0有两个不相等的实数根为x1,x2,且满足x1x2﹣2(x1+x2)+4=2k﹣
=0有两个不相等的实数根为x1,x2,且满足x1x2﹣2(x1+x2)+4=2k﹣![]() ,请考虑k的取值范围前提下,求出k的值
,请考虑k的取值范围前提下,求出k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,BD平分∠ABC,过D作DE⊥BD交AB于点E,经过B,D,E三点作⊙O.
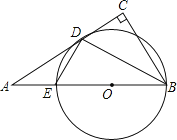
(1)求证:AC与⊙O相切于D点;
(2)若AD=15,AE=9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾分类有利于对垃圾进行分流处理,能有效提高垃圾的资源价值和经济价值,力争物尽其用,为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,某校对八年级甲,乙两班各60名学生进行了垃极分类相关知识的测试,并分别抽取了15份成绩,整理分析过程如下,请补充完整.
(收集数据)
甲班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
乙班15名学生测试成绩统计如下:《满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
(整理数据)
(1)按如下分数段整理、描述这两组样本数据
组别 频数 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
甲 | 2 | 2 | 4 | 5 | 1 | 1 |
乙 | 1 | 1 | a | b | 2 | 0 |
在表中,a= ,b= .
(2)补全甲班15名学生测试成绩频数分布直方图:
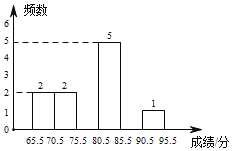
(分析数据)
(3)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 80 | x | 80 | 47.6 |
乙 | 80 | 80 | y | 26.2 |
在表中:x= ,y= .
(4)若规定得分在80分及以上(含80分)为合格,请估计乙班60名学生中垃极分类及投放相关知识合格的学生有 人.
(5)你认为哪个班的学生掌握垃圾分类相关知识的整体水平较好,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-2(k-1)x+k2 =0有两个实数根x1.x2.
(1)求实 数k的取值范围;
(2)若(x1+1)(x2+1)=2,试求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴l如图所示,则下列结论:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正确的结论是( )

A.①③ B.②③ C.②④ D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
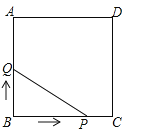
A.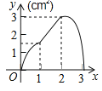 B.
B.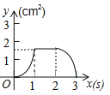 C.
C.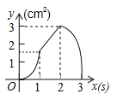 D.
D.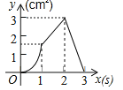
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在边AB上,点F、E在边AC上,且DF∥BE,![]() .
.

(1)求证:DE∥BC;
(2)如果![]() ,S△ADF=2,求S△ABC的值.
,S△ADF=2,求S△ABC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com