
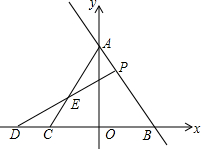
 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,点P在线段AB上,点Q是x轴负半轴上一点(在点C的左侧),且AP=CQ,PQ与线段AC交于点E
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,点P在线段AB上,点Q是x轴负半轴上一点(在点C的左侧),且AP=CQ,PQ与线段AC交于点E分析 (1)作PF∥BC交AC于F,则∠PFE=∠QCE,∠AFP=∠ACB,由AB=BC,得出∠BAC=∠ACB,证出∠AFP=∠BAC,PF=CQ,证明△PEF≌△QEC,即可得出结论;
(2)过C作PQ的平行线,交AB于点M,先求出点A、B的坐标,由勾股定理求出AB,得出BC、OC,得出C的坐标,再求出点Q的坐标,用待定系数法求出直线PQ的解析式,再求出直线CM的解析式,由直线CM和直线AB的解析式组成方程组,解方程组即可得出点M的坐标;再得出M的另一个坐标即可.
解答 解:(1)PE=QE;理由如下:
作PF∥BC交AC于F,如图1所示: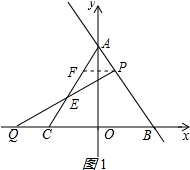
则∠PFE=∠QCE,∠AFP=∠ACB,
∵AB=BC,
∴∠BAC=∠ACB,
∴∠AFP=∠BAC,
∴AP=PF,
∵AP=CQ,
∴PF=CQ,
在△PEF和△QEC中,$\left\{\begin{array}{l}{∠PFE=∠QCE}&{\;}\\{∠PEF=∠QEC}&{\;}\\{PF=CQ}&{\;}\end{array}\right.$,
∴△PEF≌△QEC(AAS),
∴PE=QE;
(2)存在;理由如下:
分两种情况:
①当点M在中点P的下方时,过C作PQ的平行线,交AB于点M,如图2所示:
∵直线y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,
当y=0时,x=3;当x=0时,y=4;
∴B(3,0),A(0,4),
∴OA=4,OB=3,
∵∠AOB=90°,
∴AB=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴BC=AB=5,
∴OC=BC-OB=2,
∴C(-2,0),
∵点P为线段AB的中点,
∴AP=CQ=$\frac{1}{2}$AB=$\frac{5}{2}$,P($\frac{3}{2}$,2),
∴OQ=$\frac{5}{2}$+2=$\frac{9}{2}$,
∴Q(-$\frac{9}{2}$,0),
设直线PQ的解析式为:y=kx+b,
把点P($\frac{3}{2}$,2),Q(-$\frac{9}{2}$,0)代入得:$\left\{\begin{array}{l}{\frac{3}{2}k+b=2}&{\;}\\{-\frac{9}{2}k+b=0}&{\;}\end{array}\right.$,
解得:k=$\frac{1}{3}$,b=$\frac{3}{2}$,
∴直线PQ的解析式为:y=$\frac{1}{3}$x+$\frac{3}{2}$,
∵CM∥PQ,
∴设直线CM的解析式为:y=$\frac{1}{3}$x+c,
把点(-2,0)代入得:-$\frac{2}{3}$+c=0,
∴c=$\frac{2}{3}$,
∴直线CM的解析式为:y=$\frac{1}{3}$x+$\frac{2}{3}$,
解方程组$\left\{\begin{array}{l}{y=\frac{1}{3}x+\frac{2}{3}}\\{y=-\frac{4}{3}x+4}\end{array}\right.$ 得:$\left\{\begin{array}{l}{x=2}\\{y=\frac{4}{3}}\end{array}\right.$,
∴点M的坐标为:(2,$\frac{4}{3}$);
②当点M在中点P的上方时,M的坐标为(1,$\frac{8}{3}$);
∴点M的坐标为(2,$\frac{4}{3}$)或(1,$\frac{8}{3}$).
点评 本题是一次函数综合题目,考查了全等三角形的判定与性质、勾股定理、用待定系数法求一次函数的解析式、坐标与图形性质、等腰三角形的性质等知识;本题难度较大,综合性强,特别是(2)中,需要通过作辅助线用待定系数法两次求一次函数的解析式才能得出结果.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
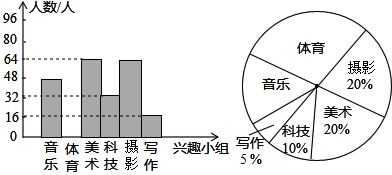
| A. | 七年级共有320人参加了兴趣小组 | |
| B. | 体育兴趣小组对应扇形圆心角的度数为96° | |
| C. | 各小组人数组成的数据的众数是64 | |
| D. | 各小组人数组成的数据的中位数是56 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
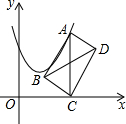 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为1.
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
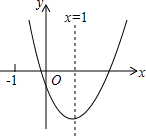 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $4\sqrt{3}-3\sqrt{3}=1$ | B. | $\sqrt{2}+\sqrt{5}=\sqrt{5}$ | C. | $2\sqrt{\frac{1}{2}}=2$ | D. | $3\sqrt{2}+2\sqrt{2}=5\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com