
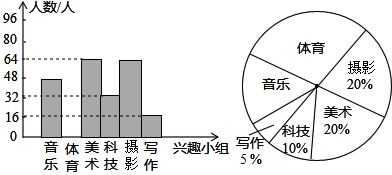
| A. | 七年级共有320人参加了兴趣小组 | |
| B. | 体育兴趣小组对应扇形圆心角的度数为96° | |
| C. | 各小组人数组成的数据的众数是64 | |
| D. | 各小组人数组成的数据的中位数是56 |
分析 总人数=参加某项的人数÷所占比例,即可判断A;
先求出体育小组所占百分比,再乘以360度求出圆心角的度数,即可判断B;
一组数据中出现次数最多的数据叫做众数,即可判断C;
将一组数据按照从小到大(或从大到小)的顺序排列,处于中间位置的数(或中间两个数据的平均数)就是这组数据的中位数,即可判断D.
解答 解:A、七年级共有32÷10%=320人参加了兴趣小组,故本选项正确;
B、体育兴趣小组对应扇形圆心角的度数为360×$\frac{320-48-64-32-64-16}{320}$=108°,故本选项错误;
C、各小组人数组成的数据的众数是64,本选项正确;
D、将各小组人数组成的数据按从小到大的顺序排列为:16,32,48,64,64,96,中间两个是分别是48,64,所以中位数是(48+64)÷2=56,故本选项正确.
故选B.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查了众数与中位数.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
 李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖.
李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
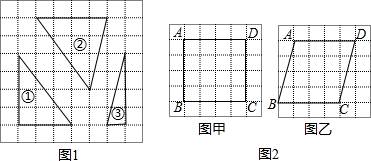
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
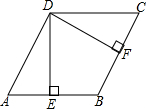 如图,已知四边形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F,在不添加其他辅助线的情况下,请你找出图中所有的全等三角形,并证明你的结论.
如图,已知四边形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F,在不添加其他辅助线的情况下,请你找出图中所有的全等三角形,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
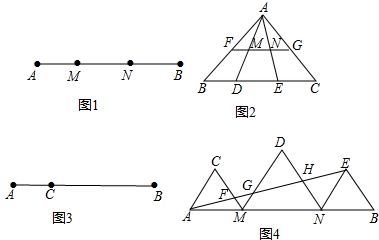
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
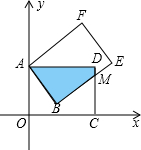 矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.
矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
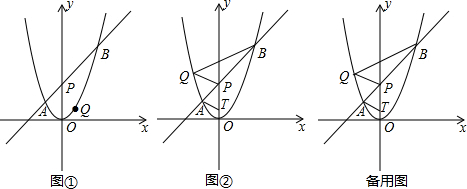
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
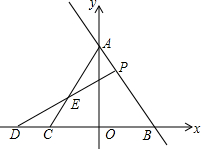 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,点P在线段AB上,点Q是x轴负半轴上一点(在点C的左侧),且AP=CQ,PQ与线段AC交于点E
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,点P在线段AB上,点Q是x轴负半轴上一点(在点C的左侧),且AP=CQ,PQ与线段AC交于点E查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com