
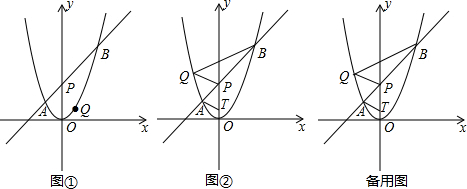
分析 (1)根据题意易得点M、P的坐标,利用待定系数法来求直线AB的解析式;
(2)如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,构建等腰直角△QDC,利用二次函数图象上点的坐标特征和二次函数最值的求法进行解答;
(3)根据相似三角形的对应角相等推知:△PBQ中必有一个内角为45°;需要分类讨论:∠PBQ=45°和∠PQB=45°;然后对这两种情况下的△PAT是否是直角三角形分别进行解答.另外,以P、B、Q为顶点的三角形与△PAT相似也有两种情况:△Q″PB∽△PAT、△Q″BP∽△PAT.
解答 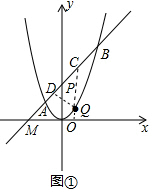 解:(1)如图①,设直线AB与x轴的交点为M.
解:(1)如图①,设直线AB与x轴的交点为M.
∵∠OPA=45°,
∴OM=OP=2,即M(-2,0).
设直线AB的解析式为y=kx+b(k≠0),将M(-2,0),P(0,2)两点坐标代入,得
$\left\{\begin{array}{l}{2=k×0+b}\\{0=k×(-2)+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$.
故直线AB的解析式为y=x+2;
(2)如图①,过点Q作x轴的垂线QC,交AB于点C,再过点Q作直线AB的垂线,垂足为D,根据条件可知△QDC为等腰直角三角形,则QD=$\frac{\sqrt{2}}{2}$QC.
设Q(m,m2),则C(m,m+2).
∴QC=m+2-m2=-(m-$\frac{1}{2}$)2+$\frac{9}{4}$,
QD=$\frac{\sqrt{2}}{2}$QC=$\frac{\sqrt{2}}{2}$[-(m-$\frac{1}{2}$)2+$\frac{9}{4}$].
故当m=$\frac{1}{2}$时,点Q到直线AB的距离最大,最大值为$\frac{9\sqrt{2}}{8}$;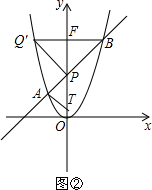
(3)∵∠APT=45°,
∴△PBQ中必有一个内角为45°,由图知,∠BPQ=45°不合题意.
①如图②,若∠PBQ=45°,过点B作x轴的平行线,与抛物线和y轴分别交于点Q′、F.此时满足∠PBQ′=45°.
∵Q′(-2,4),F(0,4),
∴此时△BPQ′是等腰直角三角形,由题意知△PAT也是等腰直角三角形.
(i)当∠PTA=90°时,得到:PT=AT=1,此时t=1;
(ii)当∠PAT=90°时,得到:PT=2,此时t=0.
②如图③,若∠PQB=45°,①中是情况之一,答案同上;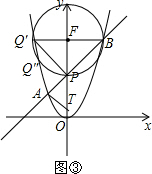
先以点F为圆心,FB为半径作圆,则P、B、Q′都在圆F上,设圆F与y轴左侧的抛物线交于另一点Q″.
则∠PQ″B=∠PQ′B=45°(同弧所对的圆周角相等),即这里的交点Q″也是符合要求.
设Q″(n,n2)(-2<n<0),由FQ″=2,得
n2+(4-n2)2=22,即n4-7n2+12=0.
解得n2=3或n2=4,而-2<n<0,故n=-$\sqrt{3}$,即Q″(-$\sqrt{3}$,3).
可证△PFQ″为等边三角形,
所以∠PFQ″=60°,又PQ″=PQ″,
所以∠PBQ″=$\frac{1}{2}$∠PFQ″=30°.
则在△PQ″B中,∠PQ″B=45°,∠PBQ″=30°.
(i)若△Q″PB∽△PAT,则过点A作y轴的垂线,垂足为E.
则ET=$\sqrt{3}$AE=$\sqrt{3}$,OE=1,
所以OT=$\sqrt{3}$-1,
解得t=1-$\sqrt{3}$;
(ii)若△Q″BP∽△PAT,则过点T作直线AB垂线,垂足为G.
设TG=a,则PG=TG=a,AG=$\sqrt{3}$TG=$\sqrt{3}$a,AP=$\sqrt{2}$,
∴$\sqrt{3}$a+a=$\sqrt{2}$,
解得PT=$\sqrt{2}$a=$\sqrt{3}$-1,
∴OT=OP-PT=3-$\sqrt{3}$,
∴t=3-$\sqrt{3}$.
综上所述,所求的t的值为t=1或t=0或t=1-$\sqrt{3}$或t=3-$\sqrt{3}$.
点评 本题考查了二次函数综合题.其中涉及到了待定系数法求一次函数解析式,二次函数图象上点的坐标特征,二次函数的最值的求法以及相似三角形的判定与性质,难度比较大.另外,解答(3)题时,一定要分类讨论,做到不重不漏.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
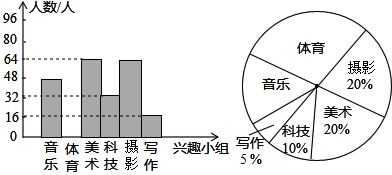
| A. | 七年级共有320人参加了兴趣小组 | |
| B. | 体育兴趣小组对应扇形圆心角的度数为96° | |
| C. | 各小组人数组成的数据的众数是64 | |
| D. | 各小组人数组成的数据的中位数是56 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
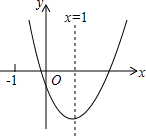 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com