
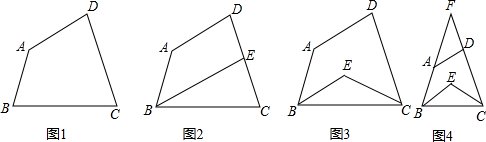
分析 (1)先根据四边形内角和等于360°求出∠B+∠C的度数,再除以2即可求解;
(2)先根据平行线的性质得到∠ABE的度数,再根据角平分线的定义得到∠ABC的度数,再根据四边形内角和等于360°求出∠BEC的度数;
(3)①先根据四边形内角和等于360°求出∠ABC+∠BCD的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数;
②先根据三角形内角和等于180°求出∠FBC+∠BCF的度数,再根据角平分线的定义得到∠EBC+∠ECB的度数,再根据三角形内角和等于180°求出∠BEC的度数
解答 解:(1)∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠B=∠C,
∴∠C=70°;
(2)∵BE∥AD,
∴∠ABE=180°-∠A=180°-145°=35°,
∵∠ABC的角平分线BE交DC于点E,
∴∠ABC=70°,
∴∠C=360°-(145°+75°+70°)=70°;
(3)①∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°-(145°+75°)=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°;
②不变.
∵∠F=40°,
∴∠FBC+∠BCF=180°-40°=140°,
∵∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°-70°=110°.
点评 本题考查了多边形内角与外角,解决的关键是综合运用四边形的内角和以及三角形的内角和、熟练运用平行线的性质和角平分线的定义.


科目:初中数学 来源: 题型:解答题
 李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖.
李叔叔刚分到一套新房,其结构如图所示(单位:m),他打算除卧室外,其余部分铺地砖. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
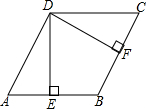 如图,已知四边形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F,在不添加其他辅助线的情况下,请你找出图中所有的全等三角形,并证明你的结论.
如图,已知四边形ABCD是菱形,DE⊥AB于点E,DF⊥BC于点F,在不添加其他辅助线的情况下,请你找出图中所有的全等三角形,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com