
分析 (1)根据函数图象的纵坐标,可得答案;
(2)根据函数图象的横坐标,可得到达书店时间,离开书店时间,根据有理数的减法,可得答案,根据函数图象的纵坐标,可得相应的路程,根据有理数的加法,可得答案;
(3)根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得速度;
(4)根据路程、速度,即可得到时间.
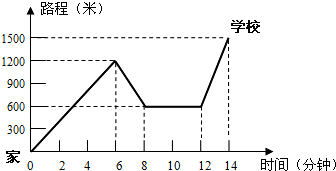
解答 解:(1)陈杰家到学校的距离是1500米,
1500-600=900(米).
答:书店到学校的距离是900米.
(2)12-8=4(分钟).
答:陈杰在书店停留了4分钟.
1200+(1200-600)+(1500-600)=2700(米).
答:本次上学途中,陈杰一共行驶了2700米
(3)(1500-600)÷(14-12)=450米/分.
答:在整个上学的途中12分钟到14分钟时段陈杰骑车速度最快,最快的速度是450米/分;
(4)1500÷(1200÷6)=7.5(分钟),14-7.5=6.5(分钟).
答:陈杰以往常的速度去学校,需要7.5分钟,本次上学比往常多用6.5分钟.
点评 本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 应试者 | 面试 | 笔试 |
| 甲 | 80 | 90 |
| 乙 | 90 | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com