
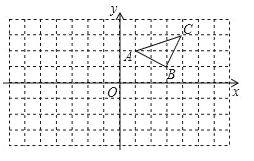
【题目】已知:如图所示.
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小,并直接写出此时PA+PC的最小值.
科目:初中数学 来源: 题型:
【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
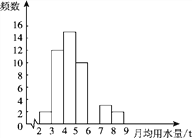
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
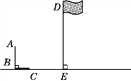
【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和告知给你代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写表格;
平均数/分 | 中位数/分 | 众数/分 | |
初中代表队 | |||
高中代表队 |
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把正六边形对角线的交点称为它的中心,正六边形的顶点及它的中心称作特征点,如图(1)有六个顶点和一个中心点,因此共有7个特征点,照图(1)的方式继续排列正六边形,使得相邻两个正六边形的一边重合,这样得到图(2),图(3)…

观察以上图形得到表:
图形的名称 | 特征点的个数 |
图1 | 7 |
图2 | 12 |
… | … |
(1)第n个图形的特征点有多少个?
(2)第100个图形的特征点有多少个?
(3)第几个图形有2017个特征点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com