
ĄŸÌâÄżĄżÎÒĂÇ°ŃŐęÁù±ßĐζԜÇÏߔĜ»”ăłÆÎȘËü”ÄÖĐĐÄŁŹŐęÁù±ßĐΔĶ„”ăŒ°Ëü”ÄÖĐĐÄłÆŚśÌŰŐś”㣏ÈçÍŒŁš1Ł©ÓĐÁùžö¶„”ășÍÒ»žöÖĐĐĔ㣏ÒòŽËčČÓĐ7žöÌŰŐś”㣏ŐŐÍŒŁš1Ł©”Ä·œÊœŒÌĐűĆĆÁĐŐęÁù±ßĐÎŁŹÊč”ĂÏàÁÚÁœžöŐęÁù±ßĐΔÄÒ»±ßÖŰșÏŁŹŐâŃù”Ă”œÍŒŁš2Ł©ŁŹÍŒŁš3Ł©Ą

čÛČìÒÔÉÏÍŒĐΔÔœ±íŁș
ÍŒĐΔÄĂûłÆ | ÌŰŐś”ă”ÄžöÊę |
͌1 | 7 |
͌2 | 12 |
Ą | Ą |
Łš1Ł©”ÚnžöÍŒĐΔÄÌŰŐś”ăÓжàÉÙžöŁż
Łš2Ł©”Ú100žöÍŒĐΔÄÌŰŐś”ăÓжàÉÙžöŁż
Łš3Ł©”ÚŒžžöÍŒĐÎÓĐ2017žöÌŰŐś”㣿Çë˔ÜÀíÓÉŁź
ĄŸŽđ°žĄżŁš1Ł©5n+2;(2)502;(3) 2017,ÀíÓÉŒûœâÎö
ĄŸœâÎöĄżŐûÌć·ÖÎöŁș
(1)”ÚÒ»žöÍŒĐÎżÉÒÔżŽłÉÊÇ5ĄÁ1+2=7žö”㣏șóĂæĂżÒ»žöÍŒĐαÈËüÇ°Ăæ”ÄÍŒĐζà5žö”㣏ÓÉŽËŒŽżÉ”Ă”œčæÂÉŁ»Łš2Ł©ÓÉŁš1Ł©ÖĐ”ÄčæÂÉœűĐĐŒÆË㣻Łš3Ł©žùŸĘŁš1Ł©ÖĐ”ÄčæÂÉŒÆË㣏ŚąÒânÒȘÊÇŐęŐûÊę.
œâŁșŁš1Ł©ĄßÍŒ1ÖĐÓĐ5ĄÁ1+2=7žö”㣏
ÍŒ2ÖĐÓĐ5ĄÁ2+2=12žö”㣏
ĄĄ
ĄàÍŒnÖĐÓĐ5n+2žöÌŰŐś”㣻
Łš2Ł©”±n=100ʱŁŹ5n+2=502ŁŹ
ŒŽ”Ú100žöÍŒĐΔÄÌŰŐś”ăÓĐ502žöŁ»
Łš3Ł©ÓÉ5n+2=2017”Ăn=403ŁŹ
ŒŽ”Ú403žöÍŒĐÎÓĐ2017žöÌŰŐś”㣟



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
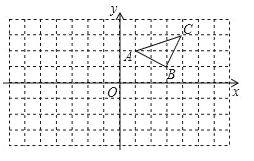
ĄŸÌâÄżĄżÒŃÖȘŁșÈçÍŒËùÊŸŁź
Łš1Ł©ŚśłöĄśABCčŰÓÚyÖá¶ÔłÆ”ÄĄśAĄäBĄäCĄäŁŹČąĐŽłöĄśAĄäBĄäCĄäÈęžö¶„”ă”ÄŚű±êŁź
Łš2Ł©ÔÚxÖáÉÏ»łö”ăPŁŹÊčPA+PCŚîĐĄŁŹČąÖ±œÓĐŽłöŽËʱPA+PC”ÄŚîĐĄÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłč€ł§œÓÊÜÁË20ÌìÄÚÉúČú1200ÌšGHĐÍ”çŚÓČúÆ·”ÄŚÜÈÎÎń. ÒŃÖȘĂżÌšGHĐÍČúÆ·ÓÉ4žöGĐÍŚ°ÖĂșÍ3žöHĐÍŚ°ÖĂĆäÌŚŚéłÉ. 耳§ÏÖÓĐ80Ăûč€ÈËŁŹĂżžöč€ÈËĂżÌìÄÜŒÓč€6žöGĐÍŚ°ÖĂ»ò3žöHĐÍŚ°ÖĂŁźč€ł§œ«ËùÓĐč€ÈË·ÖłÉÁœŚéÍŹÊ±żȘÊŒŒÓ耣ŹĂżŚé·Ö±đŒÓč€Ò»ÖÖŚ°ÖĂŁŹČąÒȘÇóĂżÌìŒÓ耔ÄGĄąHĐÍŚ°ÖĂÊęÁżŐęșĂÈ«ČżĆäÌŚŚéłÉGHĐÍČúÆ·.
Łš1Ł©°ŽŐŐŐâŃù”ÄÉúČú·œÊœŁŹč€ł§ĂżÌìÄÜĆäÌŚŚéłÉ¶àÉÙÌŚGHĐÍ”çŚÓČúÆ·Łż
Łš2Ł©ÎȘÁËÔÚč涚ÆÚÏȚÄÚÍêłÉŚÜÈÎÎńŁŹč€ł§Ÿö¶šČčłäÒ»Đ©ĐÂč€ÈËŁŹŐâĐ©ĐÂč€ÈËÖ»ÄܶÀÁąœűĐĐG ĐÍŚ°ÖĂ”ÄŒÓ耣ŹÇÒĂżÈËĂżÌìÖ»ÄÜŒÓč€4žöGĐÍŚ°ÖĂ. ÇëÎÊÖÁÉÙĐèÒȘČčłä¶àÉÙĂûĐÂč€ÈËŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔĶÁÀíœâ
Ąß![]() ŁŒ
ŁŒ![]() ŁŒ
ŁŒ![]() ŁŹŒŽ2ŁŒ
ŁŹŒŽ2ŁŒ![]() ŁŒ3Łź
ŁŒ3Łź
Ąà![]() ”ÄŐûÊęČż·ÖÎȘ2ŁŹĐĄÊęČż·ÖÎȘ
”ÄŐûÊęČż·ÖÎȘ2ŁŹĐĄÊęČż·ÖÎȘ![]() ©2ŁŹ
©2ŁŹ
Ąà1ŁŒ![]() ©1ŁŒ2
©1ŁŒ2
Ąà![]() ©1”ÄŐûÊęČż·ÖÎȘ1Łź
©1”ÄŐûÊęČż·ÖÎȘ1Łź
Ąà![]() ©1”ÄĐĄÊęČż·ÖÎȘ
©1”ÄĐĄÊęČż·ÖÎȘ![]() ©2
©2
œâŸöÎÊÌâŁșÒŃÖȘŁșaÊÇ![]() ©3”ÄŐûÊęČż·ÖŁŹbÊÇ
©3”ÄŐûÊęČż·ÖŁŹbÊÇ![]() ©3”ÄĐĄÊęČż·ÖŁŹ
©3”ÄĐĄÊęČż·ÖŁŹ
ÇóŁșŁš1Ł©aŁŹb”ÄÖ”Ł»
Łš2Ł©Łš©aŁ©3+Łšb+4Ł©2”ÄÆœ·œžùŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżčÛČìÏÂÁĐčŰÓÚŚÔÈ»Êę”Ä”ÈÊœŁș
a1Łș32-12=8ĄÁ1Ł»
a2Łș52-32=8ĄÁ2Ł»
a3Łș72-52=8ĄÁ3Ł»ĄĄ
žùŸĘÉÏÊöčæÂÉœâŸöÏÂÁĐÎÊÌâŁș
ąĆĐŽłö”Úa4žö”ÈÊœŁș___________Ł»
ąÆĐŽłöÄăČÂÏë”Ä”Úanžö”ÈÊœŁšÓĂșŹn”ÄÊœŚÓ±íÊŸŁ©ŁŹČąŃéÖ€ÆäŐęÈ·ĐÔŁ»
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎȘÁËŽÓŒŚĄąÒÒÁœĂûŃĄÊÖÖĐŃĄ°ÎÒ»ÈËČÎŒÓÉ仜±ÈÈüŁŹÏÖ¶ÔËûĂÇœűĐĐÒ»ŽÎČâŃ飏ÁœžöÈËÔÚÏàÍŹÌőŒțÏžśÉä°Đ10ŽÎŁŹÎȘÁ˱ȜÏÁœÈË”ÄłÉŒšŁŹÖÆŚśÁËÈçÏÂÍłŒÆÍŒ±íŁș

ŒŚĄąÒÒÉ仜łÉŒšÍłŒÆ±í
ÆœŸùÊę | ÖĐλÊę | ·œČî | ĂüÖĐ10»·”ÄŽÎÊę | |
ŒŚ | 7 | |||
ÒÒ | 1 |
(1)ÇëČčÈ«ÉÏÊöÍŒ±í(ÇëÖ±œÓÔÚ±íÖĐÌîżŐșÍČčÈ«ŐÛÏßÍŒ)Ł»
(2)Èçčûč涚łÉŒšœÏÎȶšŐßÊ€łöŁŹÄăÈÏÎȘËœ«Ê€łöŁżË”ĂśÄă”ÄÀíÓÉŁ»
(3)ÈçčûÏŁÍû(2)ÖĐ”ÄÁíÒ»ĂûŃĄÊÖÊ€łöŁŹžùŸĘÍŒ±íÖĐ”ÄĐĆÏąŁŹÓŠžĂÖƶšÔőŃù”ÄÆÀĆĐčæÔòŁżÎȘÊČĂŽŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚËıßĐÎABCDÖĐŁŹADĄÎBCŁŹEÎȘCD”ÄÖД㣏ÁŹœÓAEĄąBEŁŹBEĄÍAEŁŹŃÓł€AEœ»BC”ÄŃÓł€ÏßÓÚ”ăFŁź
ÇóÖ€ŁșŁš1Ł©FCŁœADŁ»
Łš2Ł©ABŁœBCŁ«ADŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘÒ»ŐĆÈęœÇĐÎÖœÆŹABCŁšÈçÍŒŒŚŁ©ŁŹÆäÖĐAB=ACŁźœ«ÖœÆŹŃŰčę”ăB”ÄÖ±ÏßŐÛ”țŁŹÊč”ăCÂ䔜AB±ßÉÏ”ÄE”㎊ŁŹŐÛșÛÎȘBDŁšÈçÍŒÒÒŁ©ŁźÔÙœ«ÖœÆŹŃŰčę”ăE”ÄÖ±ÏßŐÛ”țŁŹ”ăAÇĄșĂÓë”ăDÖŰșÏŁŹŐÛșÛÎȘEFŁšÈçÍŒ±ûŁ©ŁźÔÈęœÇĐÎÖœÆŹABCÖĐŁŹĄÏABC”ÄŽóĐĄÎȘ______ĄăŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒ1ŁŹĄśABCÖĐŁŹŃŰĄÏBAC”ÄÆœ·ÖÏßAB1ŐÛ”țŁŹŒô”ôÖŰ”țČż·ÖŁ»œ«ÓàÏÂČż·ÖŃŰĄÏB1A1C”ÄÆœ·ÖÏßA1B2ŐÛ”țŁŹŒô”ôÖŰ”țČż·ÖŁ»ĄŁ»œ«ÓàÏÂČż·ÖŃŰĄÏBnAnC”ÄÆœ·ÖÏßAnBn+1ŐÛ”țŁŹ”ăBnÓë”ăCÖŰșÏŁźÎȚÂÛŐÛ”ț¶àÉÙŽÎŁŹÖ»ÒȘŚîșóÒ»ŽÎÇĄșĂÖŰșÏŁŹÎÒĂÇŸÍłÆĄÏBACÊÇĄśABC”ÄșĂœÇŁź
ĐĄÀöŐčÊŸÁËÈ·¶šĄÏBACÊÇĄśABC”ÄșĂœÇ”ÄÁœÖÖÇéĐÎŁźÇéĐÎÒ»ŁșÈçÍŒ2ŁŹŃŰ”ÈŃüÈęœÇĐÎABC¶„œÇĄÏBAC”ÄÆœ·ÖÏßAB1ŐÛ”țŁŹ”ăBÓë”ăCÖŰșÏŁ»ÇéĐζțŁșÈçÍŒ3ŁŹŃŰĄśABC”ÄĄÏBAC”ÄÆœ·ÖÏßAB1ŐÛ”țŁŹŒô”ôÖŰ”țČż·ÖŁ»œ«ÓàÏÂČż·ÖŃŰĄÏB1A1C”ÄÆœ·ÖÏßA1B2ŐÛ”țŁŹŽËʱ”ăB1Óë”ăCÖŰșÏŁź
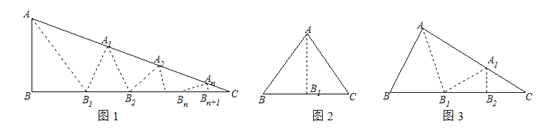
Łš1Ł©ĐĄÀöŸčęÈęŽÎŐÛ”ț·ąÏÖÁËĄÏBACÊÇĄśABC”ÄșĂœÇŁŹÇëÌœŸżĄÏBÓëĄÏCŁšČ»·ÁÉèĄÏBŁŸĄÏCŁ©ÖźŒä”Ä”ÈÁżčŰÏ”Łź
Łš2Ł©žùŸĘÒÔÉÏÄÚÈĘČÂÏëŁșÈôŸčęnŽÎŐÛ”țĄÏBACÊÇĄśABC”ÄșĂœÇŁŹÔòĄÏBÓëĄÏCŁšČ»·ÁÉèĄÏBŁŸĄÏCŁ©ÖźŒä”Ä”ÈÁżčŰÏ”ÎȘ Ł»
Łš3Ł©ÈçčûÒ»žöÈęœÇĐΔČîĐĄœÇÊÇ15ĄăŁŹÇÒÂúŚăžĂÈęœÇĐΔÄÈęžöœÇŸùÊÇŽËÈęœÇĐΔÄșĂœÇŁŹÔòŽËÈęœÇĐÎÁíÁœžöœÇ”ĶÈÊęÎȘ Łź
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com