
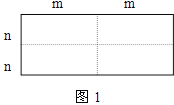
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
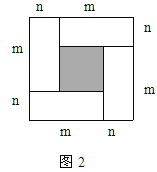
(1)你认为图2中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图2中阴影部分的面积:
方法1: ;
方法2: ;
(3)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn. ;
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,则(a-b)2== 。
【答案】(1)m-n;(2)(m+n)2-4mn、(m-n)2;(3)(m+n)2=(m-n)2+4mn;(4)29.
【解析】
试题分析:(1)观察图2,阴影部分的边长就是矩形的长与宽的差,即(m-n);
(2)本题可以直接求阴影部分正方形的边长,计算面积;也可以用正方形的面积减去四个小长方形的面积,得阴影部分的面积;
(3)由(2)即可得出三个代数式之间的等量关系;
(4)将a+b=7,ab=5,代入三个代数式之间的等量关系即可求出(a-b)2的值.
试题解析:(1)图2中的阴影部分的正方形的边长等于(m-n);
(2)方法一、阴影部分的面积=(m+n)2-2m2n;
方法二、阴影部分的边长=m-n;故阴影部分的面积=(m-n)2.
(3)三个代数式之间的等量关系是:(m+n)2=(m-n)2+4mn;
(4)(a-b)2=(a+b)2-4ab=29.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD 中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子可利用x2+(p+q)x+pq=(x+p)(x+q)分解因式的是( )
A. x2﹣3x+2 B. 3x2﹣2x+1 C. x2+x+3 D. 3x2+5x+7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
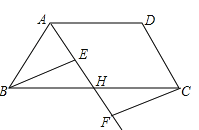
(1)请你添加一个条件,使得△BEH≌△CFH,你添加的条件是 ,并证明.
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
A.54﹣x=20%×108
B.54﹣x=20%(108+x)
C.54+x=20%×162
D.108﹣x=20%(54+x)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com