
【题目】甲、乙两件服装的成本共500元,商店老板为获取利润,决定将甲服装按50%的利润定价,乙服装按40%的利润定价.在实际出售时,应顾客要求,两件服装均按9折出售,这样商店共获利157元,求甲、乙两件服装的成本各是多少元?
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.

(1)当t=1时,正方形EFGH的边长是 ;当t=4时,正方形EFGH的边长是 ;
(2)当0<t≤3时,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点P是斜边AB的中点,点M从点C向点A匀速运动,点N从点B向点C匀速运动,已知两点同时出发,同时到达终点,连接PM、PN、MN,在整个运动过程中,△PMN的面积S与运动时间t的函数关系图象大致是( )
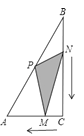

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在等腰 Rt△ABC中,∠C=90°,斜边AB=2,若将△ABC翻折,折痕EF分别交边AC、边BC于点E和点F(点E不与A点重合,点F不与B点重合),且点C落在AB边上,记作点D.过点D作DK⊥AB,交射线AC于点K,设AD=x,y=cot∠CFE,
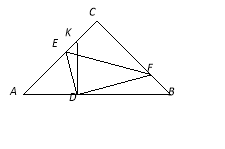

(1)求证:△DEK∽△DFB;
(2)求y关于x的函数解析式并写出定义域;
(3)联结CD,当![]() =
=![]() 时,求x的值.
时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
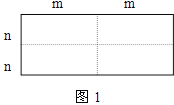
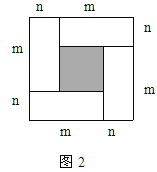
(1)你认为图2中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图2中阴影部分的面积:
方法1: ;
方法2: ;
(3)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn. ;
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,则(a-b)2== 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.

(1)求证:四边形CEDF是平行四边形;
(2)①当AE= cm时,四边形CEDF是矩形;②当AE= cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com